/Szkoła średnia/Geometria/Stereometria/Kula i sfera

Zadanie nr 6826242

Dodaj do ulubionych
Dodaj do rozwiązanych

W kulę wpisano walec w ten sposób, że objętość walca stanowi 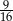-9 16 objętości kuli. Oblicz stosunek promienia kuli do wysokości walca.

Rozwiązanie

Rozpoczynamy od rysunku – od razu szkicujemy przekrój osiowy całej sytuacji.

PIC

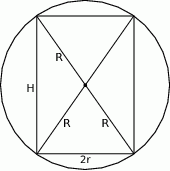
Oznaczmy przez 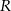R promień kuli, przez 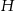H wysokość walca, a przez r promień jego podstawy. Na mocy twierdzenia Pitagorasa mamy więc

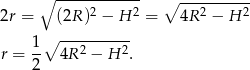
∘ ------------ 2 2 ∘ --2-----2- 2r = (2R) − H = 4R − H 1 ∘ ---------- r = 2- 4R 2 − H 2.

Z podanej informacji o objętości mamy więc równanie

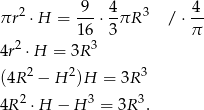
2 9-- 4- 3 4- πr ⋅H = 16 ⋅ 3πR / ⋅π 2 3 4r ⋅ H = 3R (4R 2 − H 2)H = 3R3 2 3 3 4R ⋅H − H = 3R .

W pierwszej chwili może nie być jasne co dalej z tym zrobić, ale przypomnijmy sobie co mamy obliczyć: mamy wyznaczyć 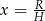x = -R H – podzielmy więc powyższą równość stronami przez 3 H .

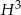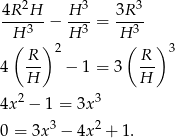
4R 2H H 3 3R 3 ------ − --- = ---- H( 3 ) H 3 H(3 ) R 2 R 3 4 -- − 1 = 3 -- H H 4x2 − 1 = 3x 3 3 2 0 = 3x − 4x + 1.

Szukamy teraz wymiernych pierwiastków – jeden widać gołym okiem: 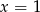x = 1 . Dzielimy więc równanie przez 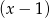(x− 1) – my robimy to grupując wyrazy.

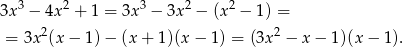
3x 3 − 4x2 + 1 = 3x3 − 3x 2 − (x 2 − 1 ) = 2 2 = 3x (x − 1) − (x + 1)(x − 1) = (3x − x− 1)(x− 1).

Szukamy teraz pierwiastków trójmianu w pierwszym nawiasie.

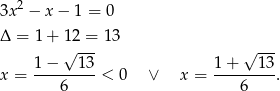
2 3x − x − 1 = 0 Δ = 1+ 12 = 13 √ --- √ --- 1-−---1-3 1-+---13- x = 6 < 0 ∨ x = 6 .

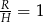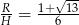Zatem RH-= 1 lub √ -- RH-= 1+6-13 .  
Odpowiedź: 1 lub 1+√-13 6

Wersja PDF