/Szkoła średnia/Geometria/Geometria analityczna/Równanie prostej/Różne

Zadanie nr 1975809

Dane są punkty 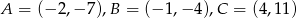A = (− 2,− 7),B = (− 1,− 4),C = (4,11) . Wykaż, że punkty te są współliniowe

Wersja PDF

Rozwiązanie

Sposób I

Wyznaczymy równanie prostej przechodzącej przez punkty 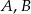A ,B , a następnie sprawdzimy czy punkt C również należy do tej prostej. Liczymy

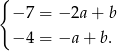
{ − 7 = − 2a + b − 4 = −a + b.

Odejmujemy stronami równania i otrzymujemy

a = 3.

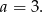
Zatem

b = − 1.

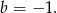
i prosta 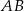AB ma równanie y = 3x − 1 .

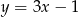Teraz podstawiamy współrzędne punktu 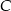C

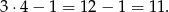
3 ⋅4 − 1 = 12 − 1 = 11.

Zatem punkt 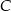C leży na prostej 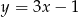y = 3x − 1 , czyli punkty 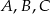A ,B,C są współliniowe.

Sposób II

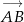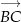Wystarczy sprawdzić, że wektory −→ AB i −→ BC są równoległe. Liczymy

−→ AB = [− 1+ 2,− 4+ 7] = [1 ,3 ] −→ BC = [4+ 1,11 + 4] = [5,15].

Widać teraz, że 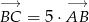−→ −→ BC = 5 ⋅AB , czyli punkty 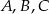A ,B,C rzeczywiście są współliniowe.

Wersja PDF