Zadanie nr 5928968
Na płaszczyźnie dane są punkty 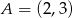 i
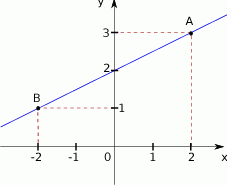
i 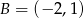 (patrz rysunek). Zbadaj, czy punkty
(patrz rysunek). Zbadaj, czy punkty 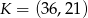 i
i 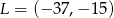 leżą po tej samej stronie prostej
leżą po tej samej stronie prostej 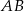 . Podaj odpowiedź i jej uzasadnienie.
. Podaj odpowiedź i jej uzasadnienie.
Rozwiązanie
Zacznijmy od napisania równania prostej 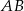 . Aby to zrobić, skorzystamy ze wzoru na prostą przechodzącą przez punkty
. Aby to zrobić, skorzystamy ze wzoru na prostą przechodzącą przez punkty 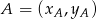 i
i 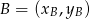 .
.
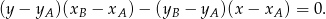
W naszej sytuacji mamy
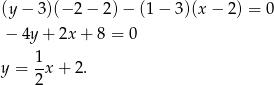
Ok, skoro mamy równanie prostej, to łatwo jest sprawdzić, czy punkt leży poniżej, powyżej czy na tej prostej. Np. dla punktu 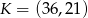 , wstawiamy
, wstawiamy 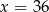 do równania prostej i dostajemy
do równania prostej i dostajemy 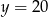 . To znaczy, że punkt na prostej o pierwszej współrzędnej
. To znaczy, że punkt na prostej o pierwszej współrzędnej 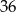 ma drugą współrzędną
ma drugą współrzędną 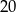 . Punkt
. Punkt 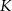 ma drugą współrzędną
ma drugą współrzędną 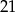 , czyli jest powyżej prostej. Podobnie sprawdzamy, że punkt
, czyli jest powyżej prostej. Podobnie sprawdzamy, że punkt 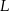 też jest powyżej prostej
też jest powyżej prostej 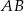 .
.
Odpowiedź: Punkty 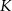 i
i 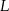 leżą po tej samej stronie prostej
leżą po tej samej stronie prostej 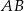 .
.

