/Konkursy/Zadania/Liczby/Całkowite/Cyfry liczb naturalnych

Zadanie nr 8483200

Niech 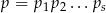p = p 1p2...ps będzie liczbą całkowitą o cyfrach 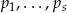p1,...,ps . Pokaż, że

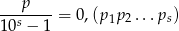
p --s-----= 0,(p 1p2...ps) 10 − 1

(okresowe rozwinięcie dziesiętne).

Wersja PDF

Rozwiązanie

Jeżeli oznaczymy

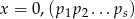
x = 0,(p 1p 2...ps)

to liczba ta ma własność

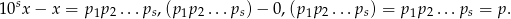
s 10 x − x = p1p2...ps ,(p1p2 ...ps)− 0 ,(p1p2...ps ) = p1p2 ...ps = p.

Przekształcenie to naśladuje standardowy sposób zamiany ułamków okresowych na ułamki zwykłe. Teraz wystarczy przekształcić otrzymaną równość

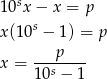
s 10 x− x = p x(10s − 1) = p p x = ---s---- 10 − 1

co kończy dowód.

Wersja PDF