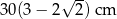/Szkoła średnia/Geometria/Stereometria/Sześcian

Zadanie nr 1721443

Do sześciennego pudła o boku długości 60 cm, włożono walec, który jest styczny do przylegających ścian. Jak dużą kulkę można jeszcze zmieścić w wolnym rogu pudła?

Wersja PDF

Rozwiązanie

Jeżeli wyobrazimy/naszkicujemy sobie opisaną sytuację, to powinno być jasne, że jeśli przetniemy cały obrazek płaszczyzną równoległą do podstaw walca i przechodzącą przez środek kulki wpisanej w róg, to dostaniemy kwadrat z dwoma wpisanymi okręgami – jeden jest styczny do wszystkich boków, a drugi do pierwszego i do dwóch boków kwadratu.

PIC

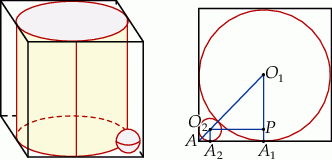
Jeżeli ktoś ma kłopoty z wyobrażeniem sobie tego, to można sobie myśleć, że patrzymy na pudełko z góry – wzdłuż osi walca.

W ten sposób zamiast zadania przestrzennego mamy zadanie z planimetrii – wystarczy obliczyć jaki jest promień małego okręgu – a to można zrobić na różne sposoby. Oznaczmy promienie okręgów przez 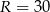R = 30 i r .

Sposób I

Jeżeli popatrzymy na mały równoramienny trójkącik prostokątny 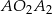AO 2A 2 , to mamy

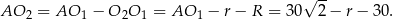
√ -- AO 2 = AO 1 − O 2O1 = AO 1 − r− R = 30 2− r− 30 .

Z drugiej strony

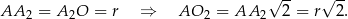
√ -- √ -- AA 2 = A 2O = r ⇒ AO 2 = AA 2 2 = r 2.

Mamy zatem

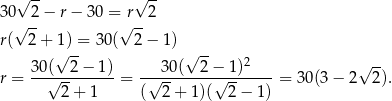
30√ 2-− r − 30 = r√ 2- √ -- √ -- r( 2 + 1) = 30( 2 − 1 ) √ -- √ -- 2 r = 30√(--2−--1) = -√-30-(--2−√-1-)----= 30(3 − 2√ 2). 2 + 1 ( 2 + 1)( 2 − 1 )

Sposób II

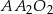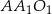Trójkąty AA 2O 2 i AA 1O1 są podobne, zatem

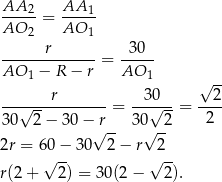
AA AA ---2-= ----1 AO 2 AO 1 ------r------ -30-- AO − R − r = AO 1 1 √ -- -------r------- -3-0-- --2- 30√ 2 − 30 − r = 30√ 2 = 2 √ -- √ -- 2r = 60 − 30 2 − r 2 √ -- √ -- r(2+ 2) = 30(2 − 2).

Zatem

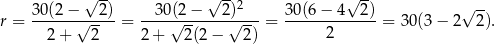
√ -- √ -- 2 √ -- √ -- r = 30(2-−√--2-)= --30(√2-−---2√)---= 30(6-−-4--2-)= 30(3 − 2 2 ). 2 + 2 2 + 2(2 − 2) 2

Sposób III

Tym razem popatrzmy na trójkąt 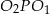O 2PO 1 . Jest to równoramienny trójkąt prostokątny, więc

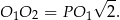
√ -- O O = P O 2. 1 2 1

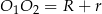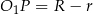Z drugiej strony O O = R + r 1 2 i O P = R − r 1 . Zatem

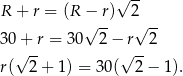
√ -- R + r = (R − r) 2 √ -- √ -- 3 0+ r = 30 2 − r 2 √ -- √ -- r( 2 + 1) = 30( 2− 1).

Stąd

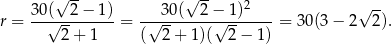
√ -- √ -- 2 √ -- r = 30√(--2−--1) = -√-30-(--2−√-1-)----= 30(3 − 2 2). 2 + 1 ( 2 + 1)( 2 − 1 )

 
Odpowiedź: Maksymalny promień kuli: √ -- 30 (3− 2 2) cm

Wersja PDF