Zadanie nr 2576268

Dany jest sześcian 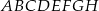ABCDEF GH , w którym 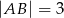|AB | = 3 (patrz rysunek). Oblicz odległość wierzchołka 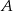od przekątnej .

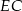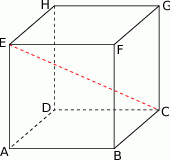
Rozwiązanie

Dorysujmy przekątne podstaw sześcianu.

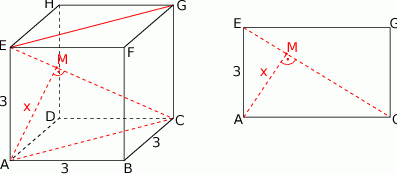
Odcinek 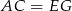AC = EG jest przekątną kwadratu o boku długości 3, więc

√ -- AC = 3 2.

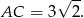
Teraz możemy obliczyć z twierdzenia Pitagorasa długość przekątnej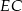

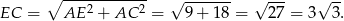
∘ ------------ √ ------- √ --- √ -- EC = AE 2 + AC 2 = 9+ 18 = 27 = 3 3.

Zauważmy, że mamy obliczyć długość wysokości 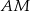w trójkącie prostokątnym ACE .

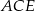Sposób I

Obliczmy pole trójkąta 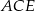ACE na dwa sposoby.

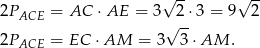
√ -- √ -- 2PACE = AC ⋅ AE = 3 2 ⋅3 = 9 2 √ -- 2PACE = EC ⋅AM = 3 3⋅ AM .

Mamy zatem

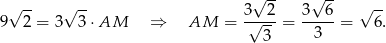
√ -- √ -- √ -- √ -- √ -- 9 2 = 3 3 ⋅AM ⇒ AM = 3√--2-= 3--6-= 6. 3 3

Sposób II

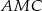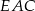Trójkąty AMC i EAC oba są prostokątne i mają jeden wspólny kąt, więc są podobne. Otrzymujemy stąd

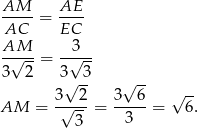
AM---= AE-- AC EC AM--- -3--- 3√ 2-= 3√ 3- √ -- √ -- 3--2- 3--6- √ -- AM = √ 3-= 3 = 6.

Odpowiedź: √ -- 6