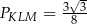Zadanie nr 5458870
Punkty 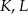 i
i 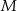 są środkami krawędzi
są środkami krawędzi 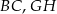 i
i 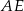 sześcianu
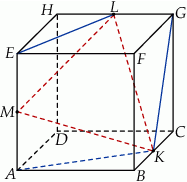
sześcianu 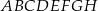 o krawędzi długości 1 (zobacz rysunek). Oblicz pole trójkąta
o krawędzi długości 1 (zobacz rysunek). Oblicz pole trójkąta 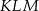 .
.
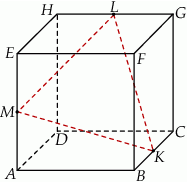
Rozwiązanie
Dorysujmy odcinki 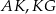 i
i 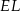 .
.
Trzy otrzymane trójkąty 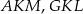 i
i 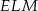 są przystające, więc
są przystające, więc 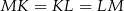 , co oznacza, że trójkąt
, co oznacza, że trójkąt 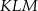 jest równoboczny. Obliczmy długość jego boku.
jest równoboczny. Obliczmy długość jego boku.
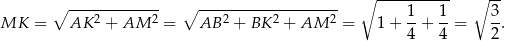
Ze wzoru na pole trójkąta równobocznego mamy
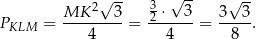
Odpowiedź: