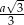/Szkoła średnia/Geometria/Stereometria/Sześcian/Różne

Zadanie nr 5664988

Dodaj do ulubionych
Dodaj do rozwiązanych

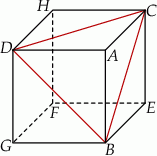
W narysowanym obok sześcianie krawędź ma długość a . Oblicz odległość wierzchołka 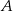A od płaszczyzny przechodzącej przez wierzchołki 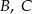B, C i D .

PIC

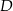Rozwiązanie

Oznaczmy szukaną odległość przez 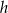h i narysujmy trochę dokładniejszy rysunek.

PIC

Sposób I

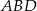Najprościej jest skorzystać ze wzoru na objętość ostrosłupa. Jeżeli popatrzymy na ostrosłup ABCD jak na ostrosłup podstawie ABD i wysokości 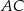AC to mamy

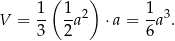
( ) 1- 1-2 1- 3 V = 3 2a ⋅ a = 6a .

Z drugiej strony, możemy myśleć, że podstawą jest trójkąt 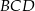BCD . Jest on równoboczny z bokiem długości 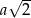√ -- a 2 , więc ma pole

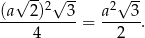
√ --2√ -- 2√ -- (a--2)---3-= a---3-. 4 2

Mamy zatem równanie

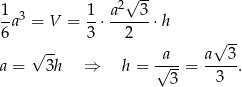
2√ -- 1a3 = V = 1-⋅ a---3⋅ h 6 3 2 -- √ -- a a√ 3 a = 3h ⇒ h = √---= ----. 3 3

Sposób II

Szukaną odległość można też policzyć bardziej bezpośrednio, z trójkąta prostokątnego 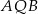AQB , Odcinek 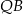QB stanowi 2 3 wysokości trójkąta równobocznego BCD . Zatem

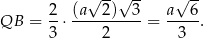
2 (a√ 2)√ 3- a√ 6- QB = -⋅ ----------= ----. 3 2 3

Mamy więc

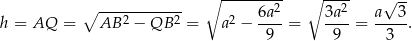
∘ ------------ ∘ -------2- ∘ ---2 √ -- h = AQ = AB 2 − QB 2 = a2 − 6a--= 3a--= a--3-. 9 9 3

 
Odpowiedź: √ - a-33

Wersja PDF