Zadanie nr 6984843
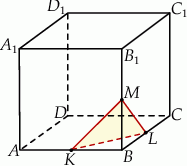
Przez środki trzech różnych krawędzi sześcianu 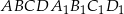 wychodzących z wierzchołka
wychodzących z wierzchołka 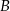 poprowadzono płaszczyznę, która wyznaczyła przekrój bryły – trójkąt
poprowadzono płaszczyznę, która wyznaczyła przekrój bryły – trójkąt 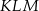 . Oblicz odległość wierzchołka
. Oblicz odległość wierzchołka 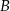 od tego przekroju, jeżeli wiadomo, że długość krawędzi sześcianu wynosi 8.
od tego przekroju, jeżeli wiadomo, że długość krawędzi sześcianu wynosi 8.
Rozwiązanie
Zauważmy, że na naroże 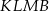 możemy patrzeć jak na ostrosłup prawidłowy trójkątny, w którym krawędzie boczne mają długość
możemy patrzeć jak na ostrosłup prawidłowy trójkątny, w którym krawędzie boczne mają długość 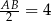 , a krawędzie podstawy długość
, a krawędzie podstawy długość 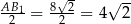 . Do obliczenia mamy długość wysokości
. Do obliczenia mamy długość wysokości 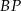 tego ostrosłupa.
tego ostrosłupa.

Sposób I
Patrzymy na trójkąt prostokątny 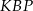 . Wiemy, że
. Wiemy, że 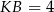 , a długość odcinka
, a długość odcinka 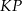 to
to  wysokości trójkąta równobocznego
wysokości trójkąta równobocznego 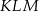 , czyli
, czyli
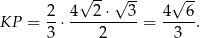
Piszemy teraz twierdzenie Pitagorasa w trójkącie 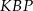 .
.
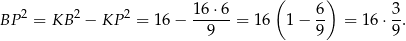
Zatem 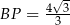 .
.
Sposób II
Długość wysokości  możemy też obliczyć licząc na dwa sposoby objętość ostrosłupa
możemy też obliczyć licząc na dwa sposoby objętość ostrosłupa 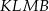 . Z jednej strony mamy
. Z jednej strony mamy
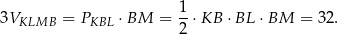
Z drugiej strony,
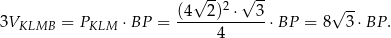
Mamy zatem
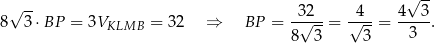
Odpowiedź: