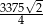Zadanie nr 8105831
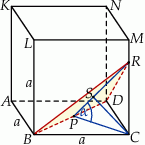
Sześcian 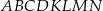 przecięto płaszczyzną przechodzącą przez przekątną
przecięto płaszczyzną przechodzącą przez przekątną 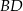 podstawy, która jest nachylona do płaszczyzny podstawy pod kątem
podstawy, która jest nachylona do płaszczyzny podstawy pod kątem  takim, że
takim, że 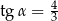 (zobacz rysunek).
(zobacz rysunek).
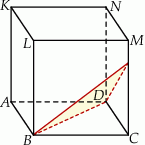
Odległość wierzchołka 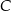 od płaszczyzny tego przekroju jest równa 6. Oblicz objętość sześcianu
od płaszczyzny tego przekroju jest równa 6. Oblicz objętość sześcianu 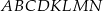 .
.
Rozwiązanie
Niech 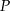 będzie środkiem podstawy a
będzie środkiem podstawy a  punktem, w którym płaszczyzna opisana w treści zadania przecina krawędź boczną sześcianu.
punktem, w którym płaszczyzna opisana w treści zadania przecina krawędź boczną sześcianu.
Przy tych oznaczeniach odległość punktu  od płaszczyzny przekroju to po prostu wysokość
od płaszczyzny przekroju to po prostu wysokość  opuszczona z wierzchołka
opuszczona z wierzchołka 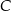 w trójkącie prostokątnym
w trójkącie prostokątnym 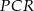 . Zanim jednak wykorzystamy tę informację, obliczmy
. Zanim jednak wykorzystamy tę informację, obliczmy 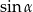 .
.
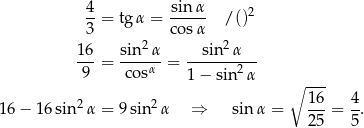
Jeżeli oznaczymy przez  długość krawędzi sześcianu, to mamy
długość krawędzi sześcianu, to mamy
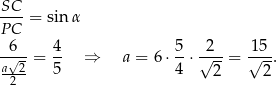
Objętość sześcianu jest więc równa
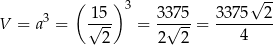
Odpowiedź: