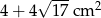/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Prawidłowy czworokątny/Pole powierzchni

Zadanie nr 6329789

Dodaj do ulubionych
Dodaj do rozwiązanych

W ostrosłupie prawidłowym czworokątnym o objętości 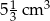1 3 53 cm wysokość jest 2 razy dłuższa od krawędzi podstawy. Oblicz pole powierzchni tego ostrosłupa

Rozwiązanie

Zaczynamy od schematycznego rysunku.

PIC

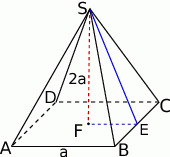
Z podanej objętości łatwo obliczamy długość krawędzi podstawy.

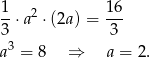
1-⋅a2 ⋅ (2a) = 16 3 3 a3 = 8 ⇒ a = 2.

Aby obliczyć pole powierzchni ostrosłupa, obliczmy wysokość ściany bocznej – stosujemy twierdzenie Pitagorasa w trójkącie F ES .

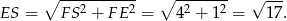
∘ --2------2- ∘ -2----2 √ --- ES = FS + F E = 4 + 1 = 17.

Zatem pole powierzchni jest równe

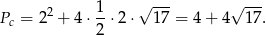
2 1 √ --- √ --- Pc = 2 + 4 ⋅--⋅2 ⋅ 17 = 4 + 4 17 . 2

 
Odpowiedź: √ --- 2 4 + 4 17 cm

Wersja PDF