Zadanie nr 7137558
Objętość ostrosłupa prawidłowego czworokątnego jest równa 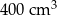 , a jego wysokość jest równa 12 cm. Oblicz pole powierzchni bocznej tego ostrosłupa. Zapisz obliczenia.
, a jego wysokość jest równa 12 cm. Oblicz pole powierzchni bocznej tego ostrosłupa. Zapisz obliczenia.
Rozwiązanie
Szkicujemy ostrosłup.
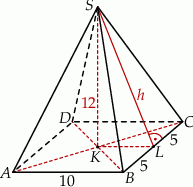
Z podanej objętości łatwo obliczyć długość  boku kwadratu w podstawie ostrosłupa.
boku kwadratu w podstawie ostrosłupa.
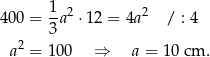
Teraz z trójkąta prostokątnego 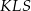 obliczamy długość wysokości
obliczamy długość wysokości 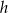 ściany bocznej ostrosłupa.
ściany bocznej ostrosłupa.
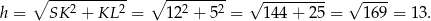
Pole powierzchni bocznej ostrosłupa jest więc równe
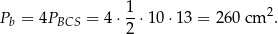
Odpowiedź: 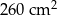 .
.

