Zadanie nr 9611474
W ostrosłupie prawidłowym czworokątnym o krawędzi podstawy 18 cm, kąt między wysokościami przeciwległych ścian bocznych ma miarę 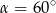 . Oblicz pole powierzchni bocznej tego ostrosłupa. Wykonaj odpowiedni rysunek i zaznacz kąt
. Oblicz pole powierzchni bocznej tego ostrosłupa. Wykonaj odpowiedni rysunek i zaznacz kąt  .
.
Rozwiązanie
Rozpoczynamy od rysunku.
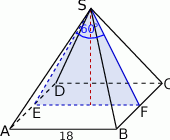
Wysokości ścian bocznych to odcinki 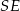 i
i 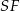 łączące wierzchołek
łączące wierzchołek 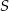 ze środkami krawędzi
ze środkami krawędzi 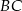 i
i 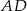 . Trójkąt
. Trójkąt 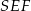 jest równoramienny i kąt między jego ramionami ma miarę
jest równoramienny i kąt między jego ramionami ma miarę 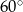 , więc jest równoboczny. W takim razie
, więc jest równoboczny. W takim razie 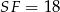 i możemy policzyć pole powierzchni bocznej ostrosłupa
i możemy policzyć pole powierzchni bocznej ostrosłupa
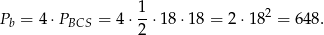
Odpowiedź: