Zadanie nr 9776118
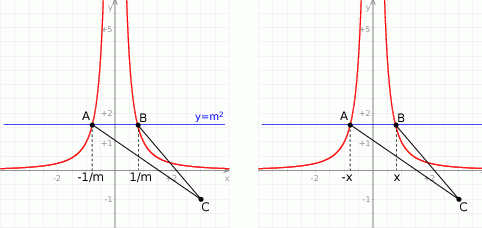
Rysunek przedstawia fragment wykresu funkcji 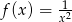 .
.
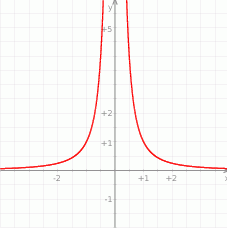
Przeprowadzono prostą równoległą do osi 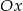 , która przecięła wykres tej funkcji w punktach
, która przecięła wykres tej funkcji w punktach 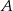 i
i 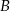 . Niech
. Niech 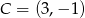 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 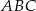 jest większe lub równe 2.
jest większe lub równe 2.
Rozwiązanie
Dorysujmy punkty 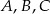 .
.
Sposób I
Powiedzmy, że pozioma prosta, o której mowa w treści zadania ma równanie 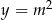 , gdzie
, gdzie 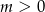 (oznaczamy
(oznaczamy 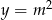 , a nie
, a nie 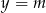 , żeby nie mieć pierwiastków przy wyliczaniu
, żeby nie mieć pierwiastków przy wyliczaniu  -ów). W takim razie punkty
-ów). W takim razie punkty 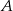 i
i 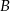 mają współrzędne:
mają współrzędne: 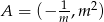 oraz
oraz 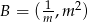 . W takim razie
. W takim razie
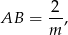
a wysokość trójkąta 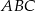 opuszczona na bok
opuszczona na bok 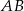 ma długość
ma długość 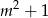 . Możemy więc policzyć pole
. Możemy więc policzyć pole
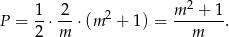
Pozostało sprawdzić, że 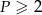 . Liczymy
. Liczymy
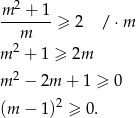
Otrzymana nierówność jest oczywiście prawdziwa co kończy uzasadnienie (bo przekształcaliśmy przy pomocy równoważności).
Sposób II
Tym razem oznaczmy pierwsze współrzędne punktów 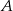 i
i 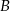 przez
przez 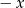 i
i  , gdzie
, gdzie 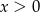 . Wtedy punkty te mają współrzędne
. Wtedy punkty te mają współrzędne 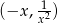 oraz
oraz 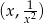 . Przy tych oznaczeniach długość odcinka
. Przy tych oznaczeniach długość odcinka 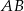 to
to 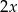 , a wysokość trójkąta
, a wysokość trójkąta 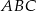 to
to 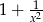 . W takim razie pole trójkąta
. W takim razie pole trójkąta 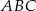 jest równe
jest równe
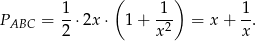
Pozostało wykazać, że liczba ta jest nie mniejsza niż 2. Przekształcamy przy pomocy równoważności.