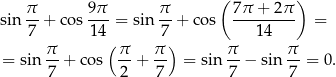/Szkoła średnia/Funkcje/Trygonometryczna/Różne

Wzory redukcyjne

Wzory redukcyjne pozwalają sprowadzić liczenie wartości funkcji trygonometrycznej dowolnego kąta do liczenia wartości funkcji trygonometrycznych kątów ostrych. Innymi słowy, jeżeli umiemy liczyć funkcje trygonometryczne dla kątów ostrych, to umiemy je liczyć dla dowolnych kątów.

Wzorów redukcyjnych jest dużo (w zasadzie nieskończenie wiele), więc nic dziwnego, że sprawiają kłopoty. Warto jednak ich się nauczyć, bo są one kluczowe w wielu zadaniach z trygonometrii. Okresowość Najprostsze wzory redukcyjne to wzory na okresowość funkcji trygonometrycznych:

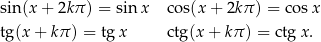
sin(x + 2kπ ) = sinx cos(x + 2k π) = co sx tg(x + kπ ) = tgx ctg(x + kπ ) = ctgx .

Te wzory są łatwe do zapamiętania i powinniśmy je stosować zupełnie automatycznie.

Obliczmy 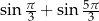sin π-+ sin 5π- 3 3 .
Liczymy

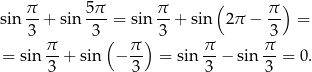
π 5 π π ( π) sin -- + sin--- = sin -- + sin 2π − -- = 3 π 3 ( π) 3 π π3 = sin --+ sin − -- = sin --− sin --= 0. 3 3 3 3

Jeżeli myślimy, że wzory na okresowość pozwalają nam przesuwać argumenty sinusa/cosinusa o wielokrotność 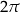2π , to pełne wzory redukcyjne pozwalają przesuwać te argumenty o wielokrotności 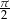π2 , czyli znacznie drobniej. Ogólne wzory redukcyjne Nie przedłużając, ogólna postać wzorów redukcyjnych jest następująca

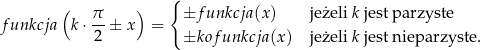
( ) { π- ±f unkcja (x) jeżeli k jest parzyste funkcja k ⋅ 2 ± x = ±kof unkcja (x) jeżeli k jest nieparzyste.

Wzór wygląda groźnie, ale postaramy się wszystko wyjaśnić.

Słowo ’funkcja’ w tym wzorze może być jedną z funkcji 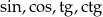sin ,cos,tg,ctg . Słowo 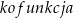kof unkcja odpowiada zamianom

sin ↔ cos tg ↔ ctg,

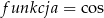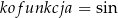czyli np. jeżeli funkcja = cos to kof unkcja = sin itd. To, czy funkcja zostaje bez zmian, czy też zamienia się na kofunkcję, zależy od parzystości 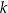k . O wyrażeniu 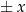± x należy myśleć, że jest to albo 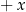+ x albo − x .

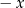Ostatnia kwestia do wyjaśnienia to znak 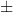± z prawej strony wzoru. W jego miejsce wpisujemy ’+’ lub ’-’ w zależności od tego, w której ćwiartce jest kąt 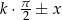π k ⋅2-± x . Przypomnijmy regułkę znaków funkcji trygonometrycznych.

W pierwszej wszystkie są dodatnie, w drugiej tylko sinus, w trzeciej tangens i cotangens, a w czwartej cosinus.

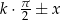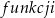Wracając do znaków, patrzymy w której ćwiartce jest kąt k⋅ π-± x 2 (przy czym o x należy myśleć jak o kącie ostrym!), z regułki patrzymy jaki jest znak funkcji (tej z lewej strony wzoru!) i taki znak piszemy z prawej strony. Przykłady Zróbmy kilka przykładów.

Wyprowadźmy wzór na 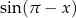sin(π − x) .
Mamy 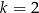k = 2 , czyli funkcja nam się nie zmieni. π − x to druga ćwiartka, czyli sinus jest dodatni. Zatem

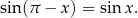
sin(π − x) = sin x.

Podobnie jest dla 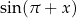sin(π + x) , ale tym razem jest to trzecia ćwiartka, czyli sinus jest ujemny. Zatem

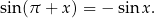
sin(π + x) = − sin x.

Wyprowadźmy wzór na 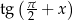( ) tg π-+ x 2 . Mamy 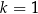k = 1 , czyli funkcja zmieni się na 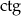ctg . Jesteśmy w drugiej ćwiartce, czyli funkcja tangens jest ujemna. Daje to nam wzór

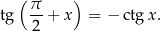
( π ) tg --+ x = − ctgx. 2

I tak dalej, idea powinna być już jasna. W ramach ćwiczeń radzę wyprowadzić sobie wzorki

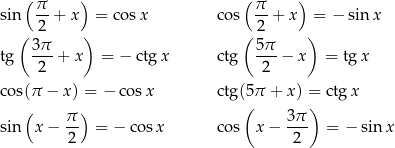
( π ) ( π ) sin --+ x = cosx cos --+ x = − sinx ( 2 ) ( 2 ) tg 3-π + x = − ctg x ctg 5π- − x = tg x 2 2 cos(π − x) = − co sx ctg((5π + x ) =) ctgx ( π-) 3-π sin x− 2 = − cosx cos x − 2 = − sin x

oraz

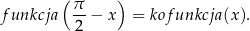
( π ) funkcja --− x = kof unkcja(x ). 2

Obliczmy 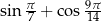sin π-+ cos 9π 7 14 .
Liczymy

( ) sin π-+ co s 9π = sin π-+ cos 7π-+--2π- = 7 14 7 14 π- (π- π-) π- π- = sin 7 + cos 2 + 7 = sin 7 − sin 7 = 0.
Powyżej wyświetlona jest tylko pierwsza część poradnika. Druga część jest dostępna tylko dla użytkowników z wykupionym abonamentem.
Zaloguj się Informacje o abonamencie
Nie chcesz się rejestrować ani opłacać abonamentu? Zapłać przelewem 7,90 zł lub telefonicznie 9,90 zł, a otrzymasz dwudziestominutowy dostęp do wszystkich materiałów dostępnych w portalu.