/Szkoła średnia/Funkcje/Trygonometryczna/Różne

Zadanie nr 6493908

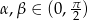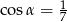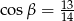Wykaż, że jeśli π- α,β ∈ (0 ,2) , 1 cos α = 7 i 13 cosβ = 14 , to π- α− β = 3 .

Wersja PDF

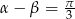Rozwiązanie

Ponieważ 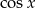cos x jest funkcją malejącą w przedziale 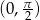π- (0,2 ) , z podanych warunków wynika, że 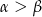α > β , czyli 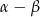α− β jest kątem ostrym. W takim razie wystarczy udowodnić, że

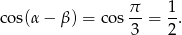
cos(α− β) = co s π = 1-. 3 2

Aby to zrobić skorzystamy ze wzoru

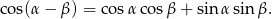
co s(α− β) = cos αco sβ + sin αsin β.

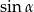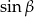Najpierw jednak musimy wyliczyć sinα i sinβ (korzystamy z tego, że są to kąty ostre!).

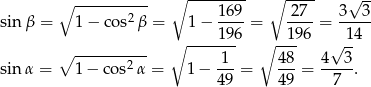
∘ -------- ∘ ---- √ -- ∘ ---------- 169 27 3 3 sin β = 1 − cos2β = 1 − ----= ----= ----- ∘ -----196 ∘ --196 √ 14 ∘ -------2-- -1- 48- 4--3- sin α = 1− cos α = 1 − 49 = 49 = 7 .

Mamy zatem

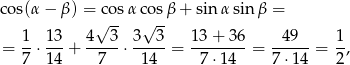
cos(α − β ) = cosα cos β + sinα sinβ = √ -- √ -- = 1-⋅ 13-+ 4--3-⋅ 3-3-= 13-+-36-= --49--= 1, 7 14 7 14 7 ⋅14 7 ⋅14 2

co kończy dowód.

Wersja PDF