/Szkoła średnia/Funkcje/Trygonometryczna/Różne

Zadanie nr 9498000

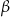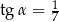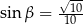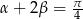Wykaż, że jeżeli α i β są kątami ostrymi, dla których 1 tgα = 7 i √-10 sin β = 10 , to α + 2β = π4- .

Wersja PDF

Rozwiązanie

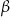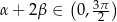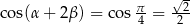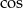Zauważmy najpierw, że jeżeli α i β są kątami ostrymi, to ( 3π) α + 2β ∈ 0 ,2 . Wystarczy w takim razie pokazać, że √ - cos(α + 2β) = cos π-= --2 4 2 (bo cos na tym przedziale tylko dla jednego argumentu przyjmuje wartość 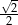√ 2 -2- ). Zauważmy jeszcze, że gdybyśmy zdecydowali się na pokazanie, że 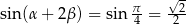√- π- -2- sin (α+ 2β) = sin 4 = 2 , to sprawa byłaby bardziej skomplikowana, bo musielibyśmy jeszcze pokazać, że 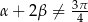3π α + 2 β ⁄= -4- . Dlatego zajmiemy się cosinusem.

Będziemy korzystać ze wzoru na cosinus sumy

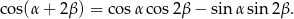
cos(α + 2β) = cosα cos 2β− sin α sin 2β .

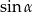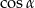Zanim jednak do tego dojdziemy obliczamy sin α i co sα z podanego tangensa.

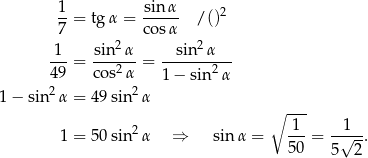
1 sin α --= tg α = ----- /()2 7 2 co sα 2 1-- -sin--α --sin-α--- 49 = co s2α = 1 − sin 2α 2 2 1− sin α = 49 sin α ∘ --- 1 1 1 = 50 sin2α ⇒ sinα = ---= -√---. 50 5 2

Stąd

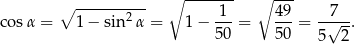
∘ ---------- ∘ ------- ∘ --- cosα = 1− sin 2α = 1 − -1-= 4-9 = -√7--. 50 5 0 5 2

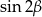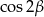Obliczamy jeszcze sin 2β i c os2β .

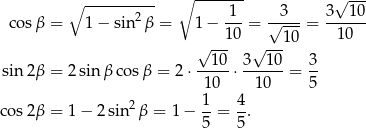
∘ ------- ∘ ---------- 1 3 3√ 10- cosβ = 1 − sin2 β = 1 − ---= √----= ------ √ --10 √ ---10 10 10 3 10 3 sin2β = 2 sin β cosβ = 2⋅ -----⋅------= -- 10 10 5 cos2β = 1 − 2sin2 β = 1 − 1-= 4-. 5 5

Mamy zatem

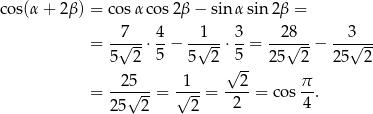
cos(α + 2 β) = cos αco s2β − sin αsin 2β = 7 4 1 3 28 3 = -√---⋅ 5-− -√---⋅ 5-= ---√--− --√--- 5 2 5 2 √ -- 25 2 25 2 --25-- -1-- --2- π- = √ --= √ -- = 2 = cos 4 . 25 2 2

Zatem rzeczywiście 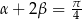π- α+ 2β = 4 .

Wersja PDF