Zadanie nr 9665010

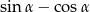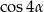Wykaż, że jeżeli sin α− cosα jest liczbą wymierną to wymierna jest również liczba cos 4α .

Rozwiązanie

Będziemy przekształcać wyrażenie 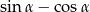sin α − cos α tak, by otrzymać 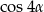cos4α . Po drodze będziemy korzystać ze wzorów

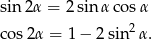
sin 2α = 2sin αcos α cos2 α = 1 − 2sin2 α.

Jeżeli oznaczymy 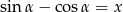sin α− cosα = x to mamy

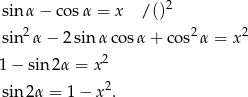
sin α− cosα = x / ()2 sin2 α− 2sinα cos α+ cos2α = x2 2 1− sin 2α = x sin 2α = 1 − x2.

A to już prawie 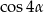co s4α , bo

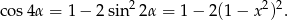
co s4α = 1− 2 sin22α = 1− 2(1 − x2)2.

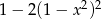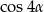Widać teraz, że jeżeli jest liczbą wymierną to wymierne jest też wyrażenie 22 1 − 2(1 − x ) , czyli co s4α .

Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!

Dodaj komentarz