Zadanie nr 4632749
Wyznacz wszystkie argumenty  , w których funkcja
, w których funkcja 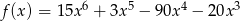 ma ekstrema lokalne.
ma ekstrema lokalne.
Rozwiązanie
Liczymy pochodną
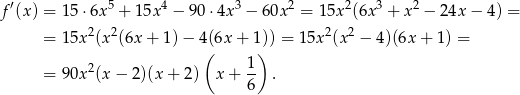
Miejsca zerowe pochodnej to: 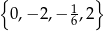 , przy czym w
, przy czym w 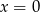 pochodna nie zmienia znaku, w
pochodna nie zmienia znaku, w 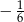 pochodna zmienia znak z dodatniego na ujemny, a w
pochodna zmienia znak z dodatniego na ujemny, a w 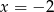 i
i 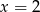 pochodna zmienia znak z ujemnego na dodatni.
pochodna zmienia znak z ujemnego na dodatni.

To oznacza, że w 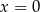 nie ma ekstremum, w
nie ma ekstremum, w 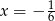 jest maksimum lokalne, a w
jest maksimum lokalne, a w 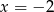 i
i 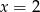 są minima lokalne.
są minima lokalne.
Na koniec, dla ciekawskich, wykres funkcji 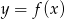 . Lewy rysunek przedstawia wykres ’z daleka’, a prawy rysunek pokazuje w powiększeniu, co się dzieje w okolicach
. Lewy rysunek przedstawia wykres ’z daleka’, a prawy rysunek pokazuje w powiększeniu, co się dzieje w okolicach 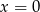 .
.
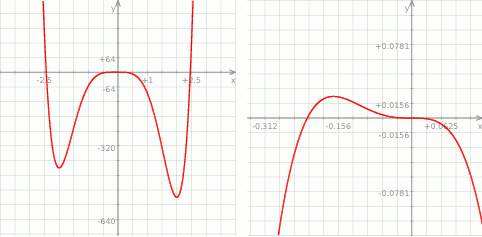
Odpowiedź: Maksimum lokalne w 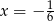 , minima lokalne w
, minima lokalne w 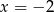 i
i 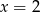 .
.

