/Studia/Analiza/Funkcje/Badanie funkcji/Pochodne/Ekstrema/Wielomiany

Zadanie nr 9795674

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz ekstrema lokalne funkcji 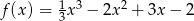1 3 2 f (x) = 3x − 2x + 3x− 2 .

Rozwiązanie

Liczymy pochodną i rozkładamy ją na czynniki.

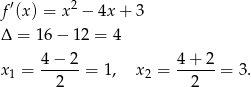
′ 2 f (x) = x − 4x + 3 Δ = 16− 12 = 4 4 − 2 4+ 2 x1 = ------= 1, x 2 = ------= 3 . 2 2

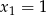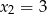Wykres pochodnej jest parabolą o ramionach skierowanych w górę i miejscach zerowych x1 = 1 i x2 = 3 . To oznacza, że funkcja przechodząc przez 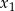x1 zmienia znak z dodatniego na ujemny, a przechodząc przez 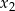x2 zmienia znak z ujemnego na dodatni. W takim razie w 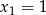x1 = 1 jest maksimum lokalne, a w 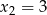x = 3 2 jest minimum lokalne. Wartości w tych punktach są równe

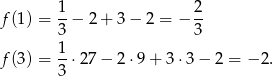
1 2 f (1) = --− 2 + 3 − 2 = − -- 3 3 f (3) = 1-⋅27 − 2 ⋅9 + 3 ⋅3− 2 = − 2. 3

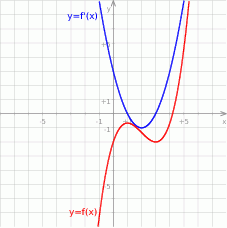
Na koniec wykres funkcji jej pochodnej.

PIC

 
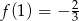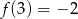Odpowiedź: Maksimum lokalne: f(1) = − 23 , minimum lokalne: f (3) = − 2 .

Wersja PDF