Definicja Wartością bezwzględną liczby  nazywamy liczbę
nazywamy liczbę
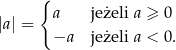
Dla osób, które tę definicję widzą pierwszy raz wyjaśnijmy, że branie wartości bezwzględnej ma polegać na odrzuceniu znajdującego się przed liczbą znaku minus. Jeżeli tego znaku minus nie ma, to branie wartości bezwzględnej nic nie zmienia.
Dokładnie taki jest sens powyższego wzoru: jeżeli liczba  jest nieujemna (czyli nie ma z przodu minusa), to
jest nieujemna (czyli nie ma z przodu minusa), to 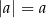 ; jeżeli natomiast liczba
; jeżeli natomiast liczba  jest ujemna, to
jest ujemna, to 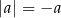 (ta operacja usuwa minus, bo dwa minusy dają plus).
(ta operacja usuwa minus, bo dwa minusy dają plus).
Licznie wartości bezwzględnej sprowadza się do ustalenia, czy liczba, z której liczymy wartość bezwzględną jest ujemna, czy też nie, np.
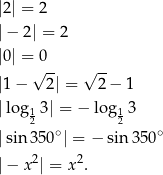
Oś liczbowa O wartości bezwzględnej liczby  warto jest myśleć w sposób geometryczny:
warto jest myśleć w sposób geometryczny:
Liczba  jest równa odległości liczby
jest równa odległości liczby  od punktu
od punktu 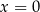 na osi liczbowej.
na osi liczbowej.

Odległość liczby 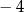 od początku osi równa się
od początku osi równa się 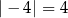 . Dokładnie taka sama jest odległość od początku osi liczby 4.
. Dokładnie taka sama jest odległość od początku osi liczby 4.
W pierwszej chwili powyższa uwaga może wydawać się dość banalna, ale ma ona niezwykle użyteczne konsekwencje:
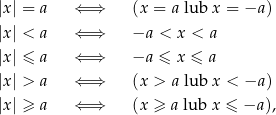
o ile 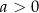 .
.
Powyższe równoważności są użyteczne, gdyż pozwalają (w prostych sytuacjach) pozbyć się wartości bezwzględnej. Zanim jednak przejdziemy do przykładów, wyjaśnijmy skąd one się wzięły.
Równość 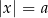 spełniają liczby
spełniają liczby  , które są odległe od 0 o
, które są odległe od 0 o  . Na osi liczbowej są dwie liczby o tej własności:
. Na osi liczbowej są dwie liczby o tej własności: 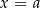 i
i 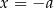 (rysunek powyżej).
(rysunek powyżej).
Nierówność 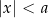 spełniają liczby, których odległość od 0 jest mniejsza niż
spełniają liczby, których odległość od 0 jest mniejsza niż  . Jest to dokładnie przedział
. Jest to dokładnie przedział 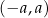 , czyli zbiór opisany nierównością
, czyli zbiór opisany nierównością 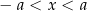 .
.

Podobnie myślimy o słabej nierówności  .
.
Nierówność 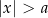 spełniają liczby, których odległość od 0 jest większa od
spełniają liczby, których odległość od 0 jest większa od  . Są to dokładnie te liczby, które znajdują się na prawo od
. Są to dokładnie te liczby, które znajdują się na prawo od  (czyli
(czyli 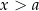 ) lub na lewo od
) lub na lewo od 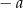 (czyli
(czyli  ). Analogiczna sytuacja ma miejsce w przypadku słabej nierówności.
). Analogiczna sytuacja ma miejsce w przypadku słabej nierówności.
Rozwiążmy równanie 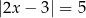 .
.
Mamy
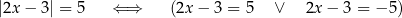
Z pierwszej równości otrzymujemy 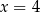 , a z drugiej
, a z drugiej 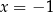 .
.
Rozwiążmy równanie 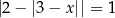 .
.
Mamy
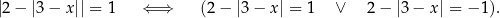
Z pierwszego równania mamy
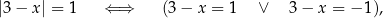
czyli 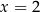 lub
lub 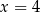 . Druga równość daje
. Druga równość daje
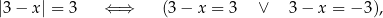
czyli 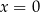 lub
lub 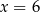 .
.
Rozwiążmy nierówność 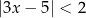 .
.
Mamy
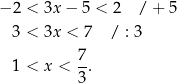
Rozwiązaniem jest więc przedział 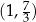 .
.
Rozwiążmy nierówność 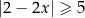 .
.
Liczymy
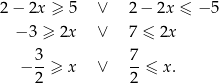
Rozwiązaniem jest więc zbiór 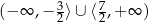 .
.
Odległość na osi Widzieliśmy przed chwilą, że myślenie o liczbie 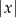 w sposób geometryczny (jako odległości na osi) pozwala w prosty sposób rozwiązać nawet dość skomplikowane zadania.
w sposób geometryczny (jako odległości na osi) pozwala w prosty sposób rozwiązać nawet dość skomplikowane zadania.
Idąc za ciosem, spróbujmy jeszcze odrobinę wytężyć naszą wyobraźnię i ustalmy, jaka jest interpretacja geometryczna liczby 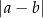 ? Odpowiedź jest niezwykle elegancka
? Odpowiedź jest niezwykle elegancka
Liczba 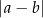 jest równa odległości na osi liczb
jest równa odległości na osi liczb  i
i 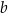 .
.
Za uzasadnienie powyższego stwierdzenia niech służy poniższy rysunek.
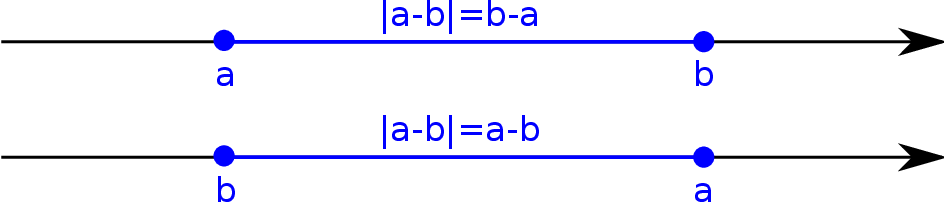
Równanie 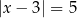 jest spełnione przez liczby
jest spełnione przez liczby  , które są odległe od liczby 3 o 5 jednostek. Gdy naszkicujemy oś liczbową, robi się jasne, że są dwie takie liczby
, które są odległe od liczby 3 o 5 jednostek. Gdy naszkicujemy oś liczbową, robi się jasne, że są dwie takie liczby 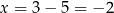 oraz
oraz 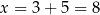 .
.

Rozwiązaniem nierówności 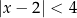 jest zbiór liczb, których odległość od 2 jest mniejsza niż 4.
jest zbiór liczb, których odległość od 2 jest mniejsza niż 4.

Jeżeli wykonamy obrazek, to widać, że jest to przedział 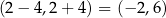
Rozwiązaniem nierówności 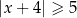 jest zbiór liczb, których odległość od -4 jest równa co najmniej 5.
jest zbiór liczb, których odległość od -4 jest równa co najmniej 5.
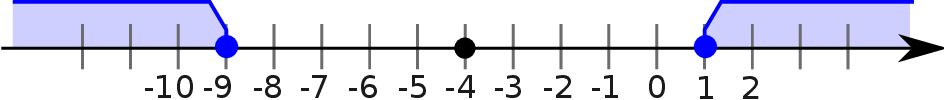
Jeżeli wykonamy obrazek, to widać, że jest to zbiór
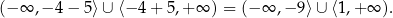
Rozwiążmy równanie 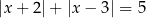 .
.
Myśląc geometrycznie, powyższe równanie oznacza: szukamy liczb  , których suma odległości od -2 i od 3 jest równa 5. Rysujemy oś liczbową i widzimy, że są dwie możliwości.
, których suma odległości od -2 i od 3 jest równa 5. Rysujemy oś liczbową i widzimy, że są dwie możliwości.
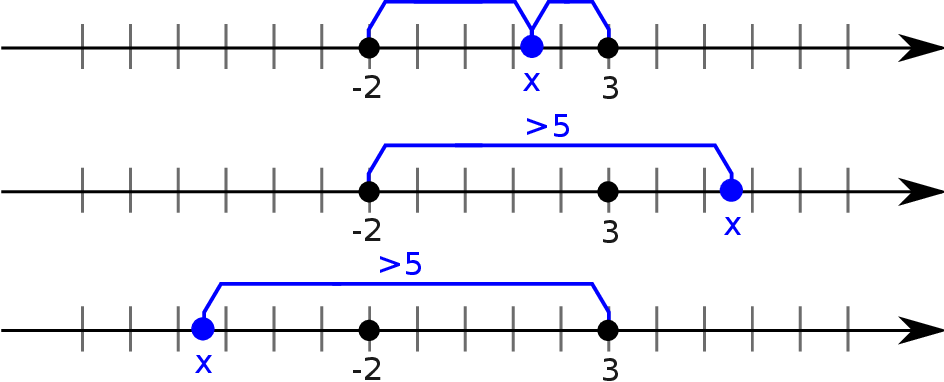
Jeżeli 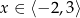 to suma odległości
to suma odległości  od -2 i 3 jest równa dokładnie długości przedziału
od -2 i 3 jest równa dokładnie długości przedziału 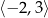 , czyli jest równa 5.
, czyli jest równa 5.
Jeżeli natomiast 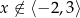 , to odległość
, to odległość  od jednego z końców tego przedziału jest większa niż 5, więc suma odległości będzie jeszcze większa.
od jednego z końców tego przedziału jest większa niż 5, więc suma odległości będzie jeszcze większa.
Rozwiązaniem równania jest więc zbiór 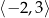 .
.
Definicja i przypadki W przypadku bardziej skomplikowanych wyrażeń z wartością bezwzględną, jedynym sposobem na pozbycie się jej, jest skorzystanie z definicji
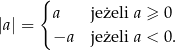
Schemat jest następujący: dla każdego wyrażenia postaci  rozważamy dwa przypadki, gdy
rozważamy dwa przypadki, gdy 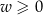 (wtedy zastępujemy
(wtedy zastępujemy  przez
przez 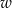 ), oraz gdy
), oraz gdy 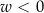 (wtedy zastępujemy
(wtedy zastępujemy  przez
przez 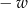 ).
).
Rozwiążmy równanie 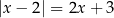 .
.
Rozważamy dwa przypadki.
Jeżeli 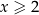 to mamy równanie
to mamy równanie

Rozwiązanie to nie spełnia założenia 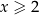 , więc je odrzucamy.
, więc je odrzucamy.
Jeżeli natomiast 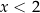 to równanie przybiera postać
to równanie przybiera postać
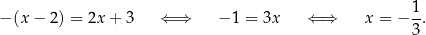
Rozwiązanie to spełnia warunek 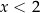 , więc jest rozwiązaniem wyjściowego równania.
, więc jest rozwiązaniem wyjściowego równania.
Rozwiążmy nierówność 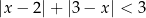 .
.
Wyrażenie pod pierwszą wartością bezwzględną jest nieujemne dla 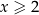 , a wyrażenie pod drugą dla
, a wyrażenie pod drugą dla 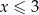 . Daje to nam 3 przypadki.
. Daje to nam 3 przypadki.
Jeżeli 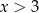 to mamy nierówność
to mamy nierówność
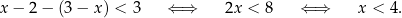
W połączeniu z warunkiem 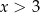 mamy w tym przypadku rozwiązanie:
mamy w tym przypadku rozwiązanie: 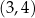 .
.
Jeżeli 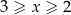 to mamy nierówność
to mamy nierówność
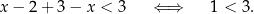
W tym przypadku nierówność jest więc spełniona tożsamościowo.
Jeżeli 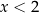 to mamy
to mamy
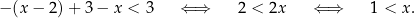
Zatem w tym przypadku mamy rozwiązanie: 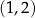 .
.
Zbierając razem rozwiązania ze wszystkich przypadków, rozwiązaniem jest zbiór 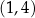 .
.
Funkcja 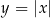 W wielu przykładach wygodnie jest myśleć o wartości bezwzględnej jako o funkcji
W wielu przykładach wygodnie jest myśleć o wartości bezwzględnej jako o funkcji 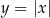 . Korzystające ze wzoru
. Korzystające ze wzoru
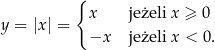
bez trudu rysujemy wykres tej funkcji
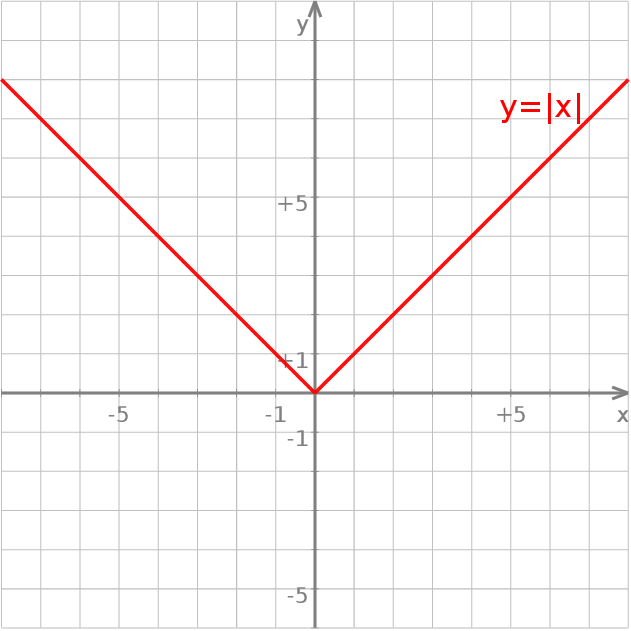
W podobny sposób rysujemy wykresy funkcji, w których wartość bezwzględna występuje w bardziej skomplikowanych wyrażeniach.
Sprawdźmy dla jakiej wartości parametru 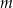 równanie
równanie
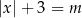
ma dwa rozwiązania.
Łatwo narysować wykres lewej strony: jest to wykres 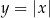 przesunięty o 3 jednostki do góry.
przesunięty o 3 jednostki do góry.
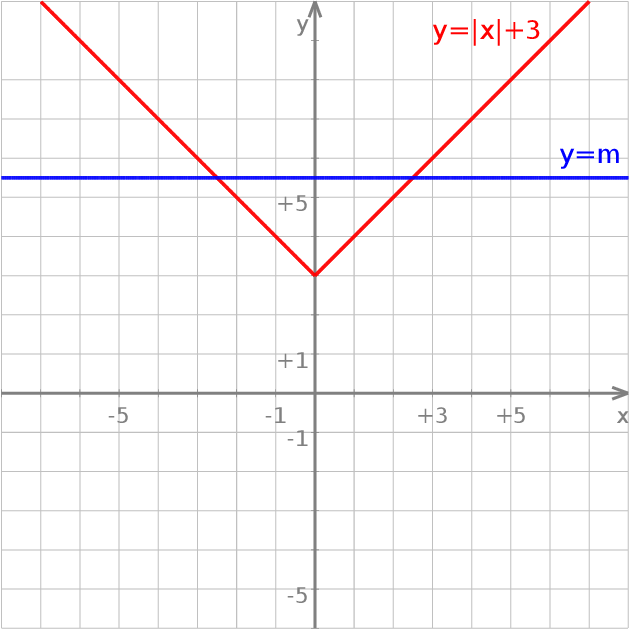
Z wykresu widać, że równanie ma dwa rozwiązania dla 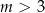 .
.
Raz jeszcze rozwiążmy nierówność 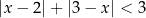 . Tym razem posłużymy się jednak wykresem lewej strony. Rysujemy wykres funkcji
. Tym razem posłużymy się jednak wykresem lewej strony. Rysujemy wykres funkcji
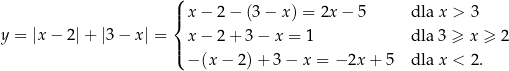
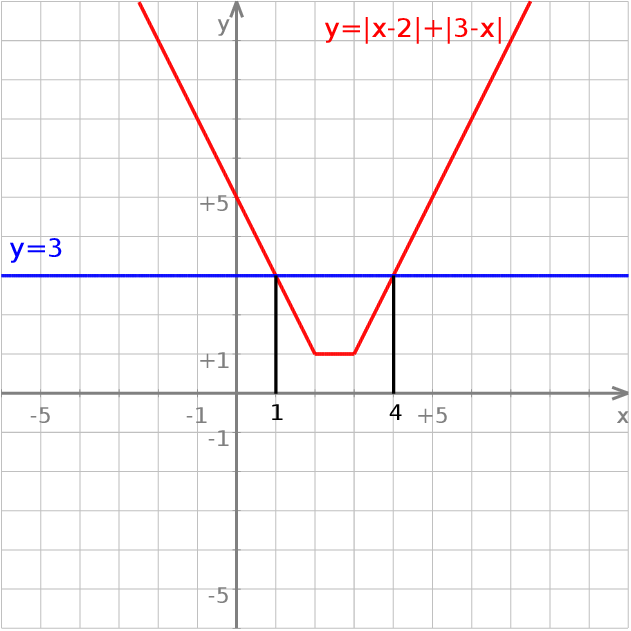
Z wykresu nie jest trudno odczytać, że rozwiązaniem nierówności jest przedział 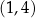 .
.

