Zadanie nr 5374242
Z podanego równania 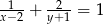 , gdzie
, gdzie 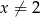 i
i 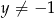 , wyznacz
, wyznacz 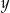 jako funkcję zmiennej
jako funkcję zmiennej  . Narysuj wykres funkcji
. Narysuj wykres funkcji 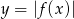 .
.
Rozwiązanie
Liczymy
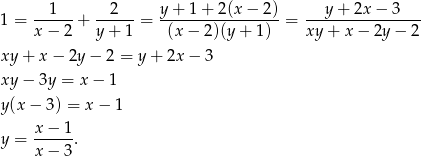
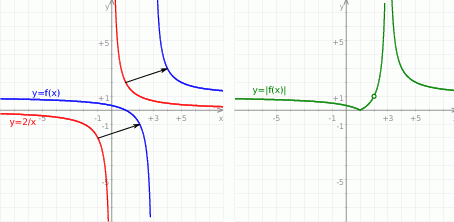
Musimy narysować wykres tej funkcji, więc przekształćmy ten wzór tak, aby pozbyć się  -a z licznika.
-a z licznika.
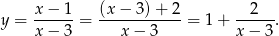
Teraz widać, że wykresem tej funkcji jest hiperbola 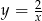 przesunięta o wektor
przesunięta o wektor ![[3,1]](https://img.zadania.info/zad/5374242/HzadR4x.gif) (o 3 jednostki w prawo i o jedną do góry). Wykres funkcji
(o 3 jednostki w prawo i o jedną do góry). Wykres funkcji 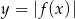 otrzymamy odbijając dodatkowo kawałek, który jest pod osią
otrzymamy odbijając dodatkowo kawałek, który jest pod osią 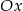 względem tej osi.
względem tej osi.