/Studia/Analiza/Funkcje/Badanie funkcji/Pochodne/Monotoniczność/Wielomiany

Zadanie nr 9941647

Dodaj do ulubionych
Dodaj do rozwiązanych

Dana jest funkcja 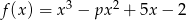3 2 f(x ) = x − px + 5x − 2 .

  • Znajdź taką wartość 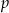p , dla której funkcja 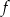f osiąga minimum w punkcie x = 5 .
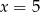  • Dla wyznaczonego 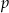p podaj przedziały monotoniczności funkcji f .

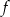Rozwiązanie

  • Liczymy pochodną danej funkcji
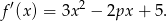
    f′(x) = 3x2 − 2px + 5.

    Jeżeli funkcja ma mieć minimum w punkcie 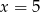x = 5 , to punkt ten musi być miejscem zerowym pochodnej, czyli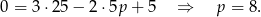

    0 = 3 ⋅25 − 2⋅ 5p + 5 ⇒ p = 8.

    Aby sprawdzić czy w punkcie 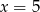x = 5 jest rzeczywiście minimum, znajdźmy drugi pierwiastek. Można to zrobić z 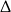Δ -y, ale prościej ze wzorów Viète’a: iloczyn pierwiastków to 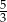5 3 , zatem drugi pierwiastek to 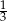1 3 . W takim razie, 5 jest większym z pierwiastków i pochodna przechodząc przez ten punkt zmienia znak z ’-’ na ’+’, czyli rzeczywiście jest minimum.  
    Odpowiedź: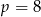 p = 8

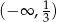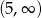  • Z poprzedniego podpunktu wiemy, że pochodna jest dodatnia na przedziałach 1 (− ∞ ,3) i (5,∞ ) oraz ujemna na 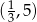1 (3,5) . Mamy zatem
    ( ⟩ f jest rosn ąca w przedzia łach − ∞ , 1 i ⟨5 ,∞ ) 3 ⟨ 1 ⟩ f jest malej ąca w przedziale --,5 . 3

     
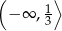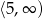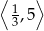    Odpowiedź: Rosnąca w ( 1⟩ − ∞ ,3 i ⟨5,∞ ) , malejąca w ⟨ ⟩ 1 3,5 .

Wersja PDF