/Konkursy/Zadania/Geometria/Planimetria/Trójkąt/Prostokątny

Zadanie nr 8995583

Dodaj do ulubionych
Dodaj do rozwiązanych

Środkowa trójkąta jest równa połowie boku, do którego została poprowadzona. Wykaż, że trójkąt ten jest prostokątny.

Rozwiązanie

Zaczynamy od rysunku.

PIC

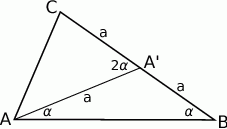
Zauważmy, że środkowa dzieli trójkąt 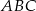ABC na dwa trójkąty równoramienne.

Sposób I

Jeżeli oznaczymy 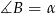∡B = α , to mamy

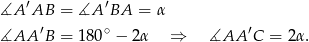
′ ′ ∡A AB = ∡A BA = α ∡AA ′B = 180∘ − 2α ⇒ ∡AA ′C = 2α .

Ponieważ 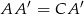AA ′ = CA ′ to

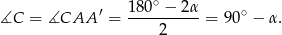
′ 180-∘ −-2-α ∘ ∡C = ∡CAA = 2 = 90 − α .

Ale w takim razie

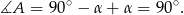
∡A = 90∘ − α + α = 90∘.

Sposób II

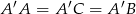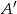Ponieważ ′ ′ ′ A A = A C = A B to ′ A jest środkiem okręgu opisanego na trójkącie 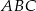ABC . W szczególności 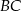BC jest średnicą okręgu opisanego, czyli 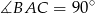∡BAC = 90∘ jako kąt oparty na średnicy.

Sposób III

Tym razem piszemy twierdzenia cosinusów w trójkątach 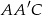′ AA C i ′ AA B .

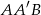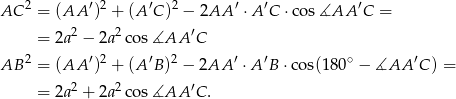
AC 2 = (AA ′)2 + (A ′C)2 − 2AA ′ ⋅A ′C ⋅cos∡AA ′C = = 2a 2 − 2a 2cos ∡AA ′C 2 ′ 2 ′ 2 ′ ′ ∘ ′ AB = (AA ) + (A B) − 2AA ⋅A B ⋅ cos(180 − ∡AA C ) = = 2a 2 + 2a 2cos ∡AA ′C.

Dodajemy te dwie równości stronami i mamy

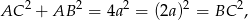
AC 2 + AB 2 = 4a2 = (2a)2 = BC 2,

co dowodzi, że trójkąt 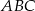ABC jest prostokątny.

Wersja PDF