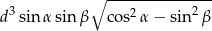/Szkoła średnia/Geometria/Stereometria/Prostopadłościan

Zadanie nr 2330944

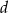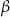Przekątna prostopadłościanu o długości d tworzy z odpowiednimi ścianami bocznymi kąty o miarach α i β . Wyznacz objętość tego prostopadłościanu.

Wersja PDF

Rozwiązanie

Zaczynamy naturalnie od dużego rysunku.

PIC

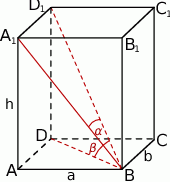
Przy oznaczeniach z rysunku mamy

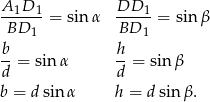
A-1D1-= sin α DD-1-= sin β BD 1 BD 1 b h --= sin α --= sinβ d d b = dsin α h = dsin β.

Ponadto

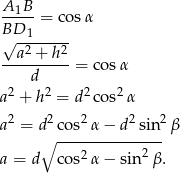
A-1B-= cosα B√D-1------ a2 + h2 ----------= co sα d a2 + h2 = d2co s2α 2 2 2 2 2 a = d∘ co-s-α-−-d--sin--β 2 2 a = d cos α − sin β .

Liczymy objętość

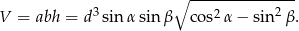
∘ --------------- V = abh = d3 sin α sin β cos2α − sin2 β.

 
Odpowiedź: ∘ --------------- d3 sin α sin β cos2α − sin2 β

Wersja PDF