/Szkoła średnia/Geometria/Stereometria/Prostopadłościan

Zadanie nr 3466953

Dodaj do ulubionych
Dodaj do rozwiązanych

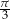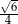Przekątne sąsiednich ścian bocznych prostopadłościanu wychodzące z jednego wierzchołka tworzą z jego podstawą kąty o miarach π3- i α . Cosinus kąta między tymi przekątnymi jest równy √- -6- 4 . Wyznacz miarę kąta α .

Rozwiązanie

Zaczynamy naturalnie od rysunku.

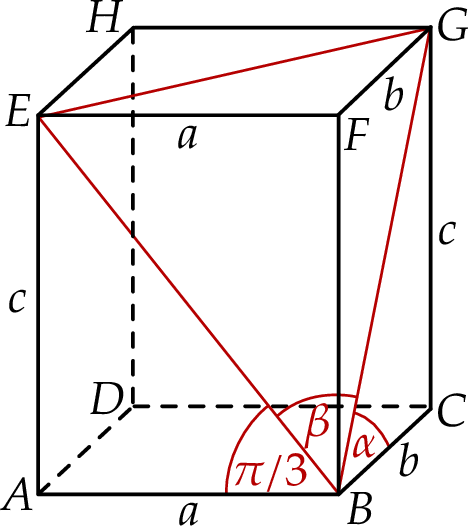
ZINFO-FIGURE

Sposób I

Spróbujmy najpierw wykorzystać podaną informację o cosinusie kąta między przekątnymi prostopadłościanu. W tym celu piszemy twierdzenie cosinusów w trójkącie 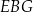EBG

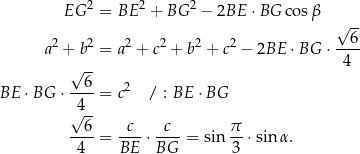
EG 2 = BE 2 + BG 2 − 2BE ⋅BG c osβ √ -- 2 2 2 2 2 2 --6- a + b = a + c + b + c − 2BE ⋅BG ⋅ 4 √ -- BE ⋅BG ⋅ --6-= c2 / : BE ⋅ BG √4-- 6 c c π ----= ---⋅ ----= sin --⋅sin α. 4 BE BG 3

Stąd

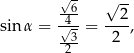
√- √ -- -64- 2 sin α = √3-= ----, -2- 2

czyli 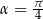α = π4- .

Sposób II

Przy oznaczeniach z rysunku mamy

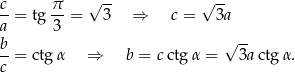
c π √ -- √ -- --= tg --= 3 ⇒ c = 3a a 3 b-= ctg α ⇒ b = c ctg α = √ 3actg α. c

Ponadto

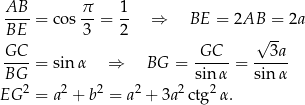
AB π 1 ----= co s-- = -- ⇒ BE = 2AB = 2a BE 3 2 √ -- GC-- GC--- --3a- BG = sin α ⇒ BG = sin α = sinα 2 2 2 2 2 2 EG = a + b = a + 3a ctg α.

Piszemy teraz twierdzenie cosinusów w trójkącie 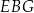EBG .

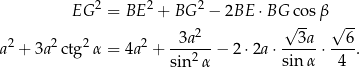
2 2 2 EG = BE + BG − 2BE ⋅BG cosβ 3a2 √ 3a √ 6- a2 + 3a2 ctg 2α = 4a 2 + ------− 2 ⋅2a ⋅-----⋅ ---. sin 2α sinα 4

Dzielimy obie strony przez 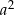2 a i mamy

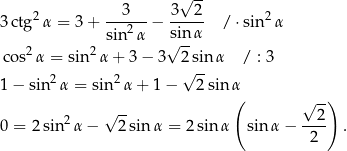
√ -- 3 ctg 2α = 3 + --3---− -3--2 /⋅ sin 2α sin 2α s√in-α co s2α = sin2 α+ 3− 3 2sin α / : 3 √ -- 1 − sin2α = sin 2α + 1 − 2 sin α ( √ -) 0 = 2 sin2α − √ 2-sin α = 2sinα sinα − --2- . 2

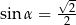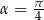Ponieważ α jest kątem ostrym, mamy stąd - √-2 sin α = 2 , czyli π- α = 4 (ponownie korzystamy z tego, że α jest ostry).  
Odpowiedź: α = π4-

Wersja PDF