Zadanie nr 4215829
Wśród uczniów pewnej szkoły przeprowadzono ankietę dotyczącą posiadanego rodzeństwa i okazało się, że:
– prawdopodobieństwo, że losowo wybrany uczeń ma brata jest równe 0,6;
– jeżeli wybierzemy losowo ucznia, który ma brata, to prawdopodobieństwo, że ten uczeń ma również siostrę jest równe 0,3;
– jeżeli wybierzemy losowo ucznia, który ma brata i ma siostrę, to prawdopodobieństwo, że ten uczeń jest uczniem klasy pierwszej jest równe 0,4.
Oblicz jakie jest prawdopodobieństwo, że losowo wybrany uczeń tej szkoły jest uczniem klasy pierwszej, który ma brata i siostrę.
Rozwiązanie
Sposób I
Wiemy, że 60% uczniów ma brata. Spośród nich 30% ma siostrę, więc
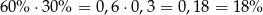
wszystkich uczniów ma brata i siostrę. Spośród tych uczniów 40% jest uczniami klas pierwszych, czyli uczniowie klas pierwszych posiadający brata i siostrę stanowią
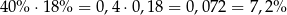
wszystkich uczniów. Takie też jest interesujące nas prawdopodobieństwo.
Sposób II
Za zdarzenia elementarne przyjmijmy zdarzenia polegające na losowym wyborze jednego ucznia. Ponadto oznaczmy: 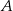 – zdarzenie polegające na wyborze ucznia, który ma brata
– zdarzenie polegające na wyborze ucznia, który ma brata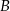 – zdarzenie polegające na wyborze ucznia, który ma siostrę
– zdarzenie polegające na wyborze ucznia, który ma siostrę – zdarzenie polegające na wyborze ucznia, który jest uczniem klasy pierwszej
– zdarzenie polegające na wyborze ucznia, który jest uczniem klasy pierwszej
Z treści zadania wiemy, że
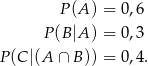
Teraz wystarczy zauważyć, że
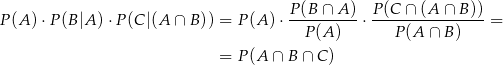
i to jest dokładnie interesujące nas prawdopodobieństwo. Mamy zatem
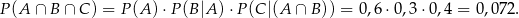
Odpowiedź: 0,072

