/Szkoła średnia/Prawdopodobieństwo/Warunkowe i całkowite/Liczba osób

Zadanie nr 4374227

Dodaj do ulubionych
Dodaj do rozwiązanych

W klasach 3a, 3b i 3c przeprowadzono sprawdzian. Losowo wybieramy klasę, a następnie ucznia z tej klasy. Jakie jest prawdopodobieństwo, że wybrany uczeń otrzymał ocenę co najmniej 4, jeżeli wiadomo, że
w klasie 3a: wszystkich uczniów jest 20, uczniów z oceną co najmiej cztery jest 8;
w klasie 3b: wszystkich uczniów jest 21, uczniów z oceną co najmiej cztery jest 14;
w klasie 3c: wszystkich uczniów jest 18, uczniów z oceną co najmiej cztery jest 6.

Rozwiązanie

Sposób I

Szukane prawdopodobieństwo 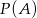P(A ) możemy rozbić na trzy prawdopodobieństwa warunkowe 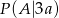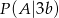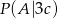P (A|3a) , P(A |3b) , P (A|3c) , gdzie warunkiem jest, że wylosowany uczeń chodzi do klasy 3a, 3b i 3c odpowiednio. Ze wzoru na prawdopodobieństwo całkowite mamy

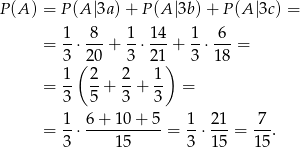
P (A ) = P(A |3a) + P(A |3b) + P(A |3c) = = 1-⋅-8-+ 1-⋅ 14-+ 1⋅ 6--= 3 (20 3 21) 3 18 1- 2- 2- 1- = 3 5 + 3 + 3 = = 1-⋅ 6-+-10-+-5-= 1-⋅ 21-= -7-. 3 15 3 15 15

Sposób II

Zamiast używać prawdopodobieństwa warunkowego i całkowitego, możemy narysować drzewko, w którym czerwone wierzchołki odpowiadają uczniom z oceną co najmniej 4 w poszczególnych klasach. Szukane prawdopodobieństwo odczytujemy z drzewka.

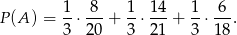
1 8 1 1 4 1 6 P(A ) = --⋅ ---+ --⋅---+ --⋅---. 3 20 3 2 1 3 18

Oczywiście jest to sama suma co w poprzednim sposobie.

PIC

 
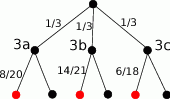
Odpowiedź: -7 15

Wersja PDF