/Szkoła średnia/Prawdopodobieństwo/Warunkowe i całkowite/Liczba osób

Zadanie nr 5486034

W klasie IIIA jest 12 dziewcząt i 14 chłopców, natomiast w klasie IIIB jest 10 dziewcząt i 16 chłopców. Rzucamy cztery razy sześcienną kostką do gry. Jeśli suma wyrzuconych oczek jest liczbą parzystą i co najmniej na jednej kostce wypadła parzysta liczba oczek, to wybieramy trzyosobową delegację z klasy IIIA, w przeciwnym wypadku z klasy IIIB. Oblicz prawdopodobieństwo, że w skład delegacji wejdzie co najmniej jeden chłopiec.

Wersja PDF

Rozwiązanie

Zajmijmy się najpierw kostkami – niech 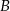B oznacza prawdopodobieństwo opisanego w treści zdarzenia polegającego na otrzymaniu (przy czterech rzutach kostką) parzystej sumy oczek i co najmniej jednej liczby parzystej. W zdarzeniach tego typu albo wszystkie cztery liczby są parzyste, albo dwie są parzyste i dwie są nieparzyste. Jest ich więc

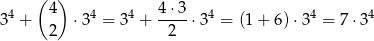
( ) 4 4 4 4 4⋅ 3 4 4 4 3 + ⋅3 = 3 + ----⋅ 3 = (1+ 6)⋅3 = 7⋅ 3 2 2

takich zdarzeń (w pierwszym przypadku na każdej kostce mamy 3 możliwości wybrania liczby parzystej, a w drugim przypadku dodatkowo musimy wybrać miejsca dla dwóch wyników parzystych). Zatem

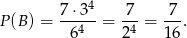
7-⋅34 7-- 7-- P (B) = 64 = 24 = 16.

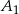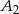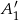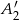Jeżeli teraz A 1 i A 2 są zdarzeniami polegającymi na tym, że jest co najmniej jeden chłopiec w delegacji wybranej odpowiednio z klasy IIIA i IIIB, to w zdarzeniach ′ A 1 i ′ A 2 wybieramy same dziewczynki, czyli

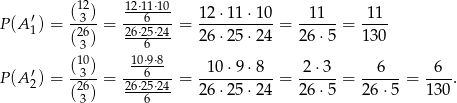
(12) 12⋅11⋅10- P(A ′1) = --3- = ---6---= 12-⋅11-⋅10-= -11---= -11- (263) 26⋅256⋅24- 26 ⋅25 ⋅24 26⋅ 5 13 0 10 10⋅9⋅8- P(A ′) = (-3) = ---6---= -10-⋅9-⋅8--= 2-⋅3--= --6---= -6--. 2 (26) 26⋅25⋅24- 26 ⋅25 ⋅24 26⋅ 5 26 ⋅5 130 3 6

Stąd

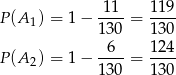
P(A ) = 1 − -11- = 1-19 1 1 30 1 30 6 1 24 P(A 2) = 1 − 1-30 = 1-30

i interesujące nas prawdopodobieństwo jest równe (wzór na prawdopodobieństwo całkowite)

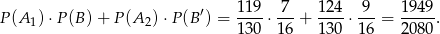
′ 11 9 7 12 4 9 1949 P(A 1) ⋅P(B )+ P (A 2)⋅P (B ) = ----⋅ ---+ ----⋅ ---= -----. 13 0 16 13 0 16 2080

 
Odpowiedź: 12904890

Wersja PDF