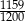Zadanie nr 8797935
Na stu mężczyzn ośmiu, zaś na tysiąc kobiet pięć ma zaburzenie rozpoznawania barw. Z grupy, w której stosunek liczby mężczyzn do liczby kobiet wynosi 7:11 wybrano losowo jedną osobę. Jakie jest prawdopodobieństwo, że wylosowana osoba prawidłowo rozpoznaje kolory?
Rozwiązanie
Jeżeli oznaczymy przez 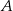 prawdopodobieństwo wylosowania osoby bez zaburzenia wzorku, oraz przez
prawdopodobieństwo wylosowania osoby bez zaburzenia wzorku, oraz przez 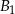 i
i 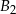 zdarzenia polegające na wylosowaniu (z danej grupy) odpowiednio mężczyzny i kobiety to wiemy, że
zdarzenia polegające na wylosowaniu (z danej grupy) odpowiednio mężczyzny i kobiety to wiemy, że
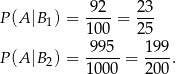
Ponadto
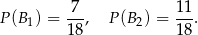
Interesujące nas prawdopodobieństwo jest więc równe (korzystamy ze wzoru na prawdopodobieństwo całkowite)
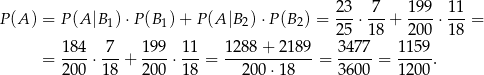
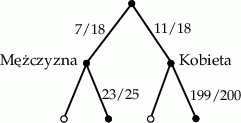
Oczywiście to samo mogliśmy odczytać z drzewka
Odpowiedź: