/Konkursy/Zadania/Geometria/Planimetria/Trapez/Długości odcinków

Zadanie nr 2518944

Dodaj do ulubionych
Dodaj do rozwiązanych

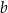Długości podstaw trapezu równoramiennego są równe a oraz b , przy czym 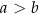a > b . W ten trapez można wpisać okrąg. Wykaż, że pole tego trapezu jest większe od a ⋅b .

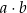Rozwiązanie

Zaczynamy od rysunku.

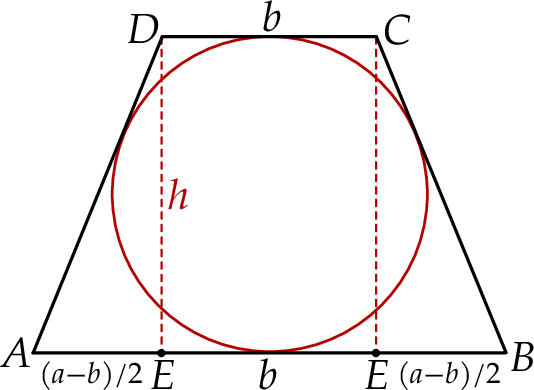
ZINFO-FIGURE

Wiem, że trapez można wpisać okrąg, więc

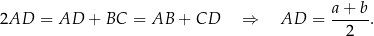
2AD = AD + BC = AB + CD ⇒ AD = a+--b. 2

Ponadto

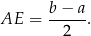
b-−-a- AE = 2 .

Napiszmy teraz twierdzenie Pitagorasa w trójkącie 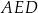AED .

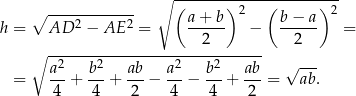
∘ (-------)2---(------)-2 ∘ ----2------2 a-+-b- b-−-a- h = AD − AE = 2 − 2 = ∘ ------------------------------ a2- b2- ab- a-2 b2- ab- √ --- = 4 + 4 + 2 − 4 − 4 + 2 = ab.

Pole trapezu jest więc równe

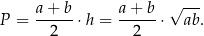
a+--b- a-+-b- √ --- P = 2 ⋅h = 2 ⋅ ab.

Pozostało więc udowodnić nierówność

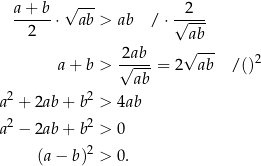
a+ b √ --- 2 --2---⋅ ab > ab / ⋅√---- ab √2ab- √ --- 2 a+ b > ab = 2 ab /() 2 2 a + 2ab + b > 4ab a2 − 2ab + b2 > 0 (a − b)2 > 0.

Otrzymana nierówność jest oczywiście spełniona (bo 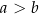a > b ), a przekształcaliśmy ją w sposób równoważny, więc wyjściowa nierówność też musiała być spełniona.

Wersja PDF