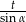Zadanie nr 3277987
W pewnym trapezie kąty przy dwóch przeciwległych wierzchołkach mają miary  oraz
oraz 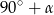 . Jedno z ramion tego trapezu ma długość
. Jedno z ramion tego trapezu ma długość 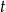 . Wyznacz różnicę długości podstaw tego trapezu.
. Wyznacz różnicę długości podstaw tego trapezu.
Rozwiązanie
Rozpoczynamy od rysunku.
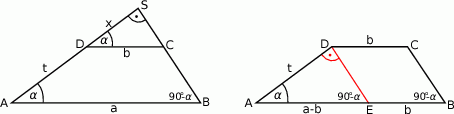
Z treści zadania nie wynika jednoznacznie, które ramię ma długość 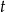 , ani który kąt ma miarę
, ani który kąt ma miarę  , ale na razie się tym nie przejmujmy – zajmiemy się tym na samym końcu.
, ale na razie się tym nie przejmujmy – zajmiemy się tym na samym końcu.
Ponieważ 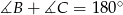 , warunek
, warunek 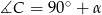 oznacza, że
oznacza, że 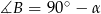 .
.
Sposób I
Jeżeli przedłużymy ramiona trapezu tak, aby się przecięły w punkcie 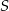 , to otrzymamy trójkąt prostokątny
, to otrzymamy trójkąt prostokątny 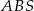 (bo
(bo 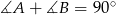 ). Prostokątny jest też trójkąt
). Prostokątny jest też trójkąt 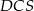 , więc przy oznaczeniach z rysunku mamy
, więc przy oznaczeniach z rysunku mamy
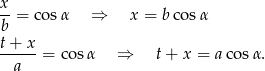
Podstawiając 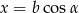 z pierwszej równości do drugiej, mamy
z pierwszej równości do drugiej, mamy
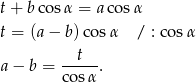
Sposób II
Tym razem dorysujmy odcinek 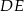 równoległy do ramienia
równoległy do ramienia 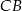 . Otrzymany trójkąt
. Otrzymany trójkąt 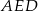 jest prostokątny (bo
jest prostokątny (bo 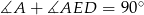 ) oraz
) oraz 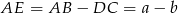 . Mamy więc
. Mamy więc
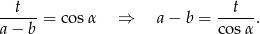
Na zakończenie zastanówmy się co się dzieje, gdy ramię długości 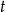 nie jest przyległe do
nie jest przyległe do  , ale do
, ale do 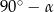 . W takiej sytuacji wszystkie nasze rachunki pozostają bez zmian, o ile tylko zmienimy wszędzie
. W takiej sytuacji wszystkie nasze rachunki pozostają bez zmian, o ile tylko zmienimy wszędzie  na
na 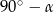 . W szczególności szukana różnica podstaw będzie wtedy równa
. W szczególności szukana różnica podstaw będzie wtedy równa
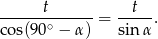
Odpowiedź: 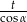 lub
lub