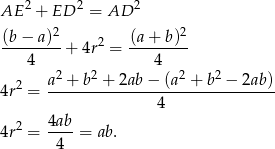Zadanie nr 9585685
Trapez równoramienny 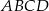 o podstawach
o podstawach 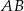 i
i 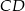 jest opisany na okręgu o promieniu
jest opisany na okręgu o promieniu  . Wykaż, że
. Wykaż, że 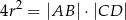 .
.
Rozwiązanie
Zaczynamy od rysunku.
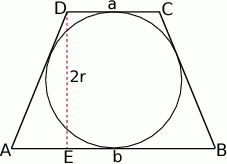
Jeżeli  i
i 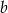 są długościami podstaw trapezu, to ponieważ w trapez można wpisać okrąg, to
są długościami podstaw trapezu, to ponieważ w trapez można wpisać okrąg, to
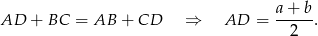
Ponadto
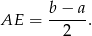
Napiszmy teraz twierdzenie Pitagorasa w trójkącie 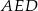 .
.