/Konkursy/Zadania/Zadania z treścią/Zadania z liczbą osób

Zadanie nr 3215763

Dodaj do ulubionych
Dodaj do rozwiązanych

W pewnej szkole 40 uczniów to członkowie SKS-u. Wśród nich 26 gra w siatkówkę, 25 pływa, a 27 jeździ na nartach. Jednocześnie pływa i gra w siatkówkę 15 uczniów, gra w siatkówkę i jeździ na nartach 16, a pływa i jeździ na nartach 18. Jeden uczeń nie zajmuje się sportem. Ilu uczniów uprawia wszystkie trzy dyscypliny sportowe? Ilu uczniów uprawia tylko jedną dyscyplinę sportową?

Rozwiązanie

Jeżeli oznaczymy przez x liczbę uczniów, którzy uprawiają wszystkie sporty na raz, to możemy policzyć ilu uczniów uprawia tylko jeden sport.

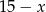Na początek zastanówmy się ile uczniów gra tylko w siatkówkę? Wiemy, że w sumie jest ich 26. Z tego x uprawia wszystkie sporty, 1 5− x uprawia dokładnie pływanie i siatkówkę, oraz 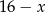16− x uprawia dokładnie narciarstwo i siatkówkę. W sumie daje nam to

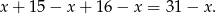
x + 15 − x + 16 − x = 31 − x.

Zatem tylko w siatkówkę gra

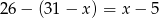
26 − (31 − x) = x− 5

uczniów.

Podobnie wyliczamy, że tylko narciarstwem interesuje się

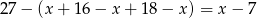
2 7− (x+ 16− x+ 18− x) = x − 7

uczniów. Natomiast tylko pływaniem zajmuje się

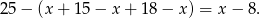
25 − (x + 15 − x + 1 8− x) = x − 8.

Teraz pozostało policzyć wszystkich uczniów.

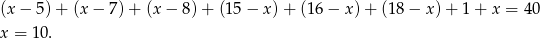
(x − 5) + (x − 7) + (x − 8) + (15 − x) + (16 − x) + (18 − x) + 1 + x = 40 x = 1 0.

Zatem tylko jeden sport uprawia

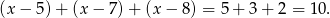
(x − 5) + (x − 7) + (x − 8) = 5+ 3+ 2 = 10.

 
Odpowiedź: 10 i 10

Wersja PDF