Zadanie nr 1380957
Wierzchołkami kwadratu 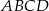 są punkty o współrzędnych
są punkty o współrzędnych 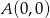 ,
, 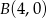 ,
, 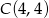 i
i 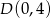 . Dla każdej liczby rzczywistej
. Dla każdej liczby rzczywistej 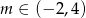 rozważamy trójkąt o wierzchołkach
rozważamy trójkąt o wierzchołkach 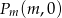 ,
, 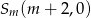 i
i 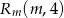 . Wyznacz wszystkie wartości prametru
. Wyznacz wszystkie wartości prametru 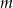 , dla których pole figury, która jest częścią wspólną kwadratu
, dla których pole figury, która jest częścią wspólną kwadratu 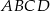 i trójkąta
i trójkąta 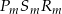 wynosi 2.
wynosi 2.
Rozwiązanie
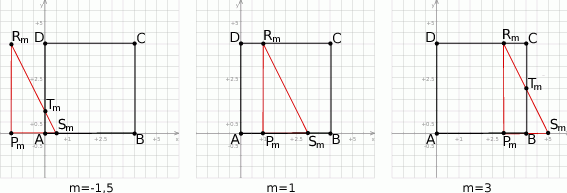
Gdy zaczniemy sobie rysować opisaną sytuację staje się jasne, że w zależności od wartości parametru 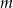 mamy trzy możliwości.
mamy trzy możliwości.
Jeżeli 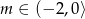 to część wspólna trójkąta
to część wspólna trójkąta 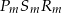 i kwadratu jest trójkątem prostokątnym
i kwadratu jest trójkątem prostokątnym 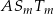 . Jest jasne, że
. Jest jasne, że 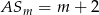 a długość drugiej przyprostokątnej
a długość drugiej przyprostokątnej 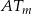 możemy wyliczyć z podobieństwa trójkątów
możemy wyliczyć z podobieństwa trójkątów 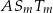 i
i 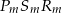
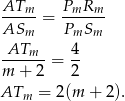
Pole tego trójkąta będzie równe 2 jeżeli
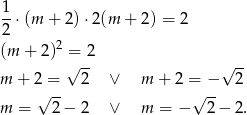
Drugi z tych pierwiastków odrzucamy, gdyż ma być 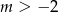 .
.
Wartość 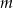 mogliśmy wyznaczyć znacznie prościej, zauważając, że z podobieństwa trójkątów
mogliśmy wyznaczyć znacznie prościej, zauważając, że z podobieństwa trójkątów 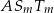 i
i 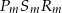 wynika, że ten pierwszy będzie miał pole równe połowie pola drugiego tylko wtedy gdy skala podobieństwa jest
wynika, że ten pierwszy będzie miał pole równe połowie pola drugiego tylko wtedy gdy skala podobieństwa jest 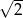 . Wtedy
. Wtedy
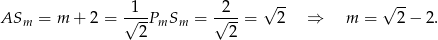
Jeżeli 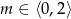 to trójkąt
to trójkąt 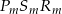 jest całkowicie zawarty w kwadracie
jest całkowicie zawarty w kwadracie 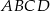 i pole stale jest równe 4.
i pole stale jest równe 4.
Jeżeli 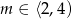 , to część wspólna podanych figur to trapez
, to część wspólna podanych figur to trapez 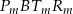 . Możemy, jak w pierwszym przypadku, policzyć pole tego trapezu, ewentualnie możemy też policzyć pole trójkąta
. Możemy, jak w pierwszym przypadku, policzyć pole tego trapezu, ewentualnie możemy też policzyć pole trójkąta 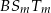 . Najprościej jest jednak, tak jak w pierwszym przypadku, skorzystać z podobieństwa trójkątów
. Najprościej jest jednak, tak jak w pierwszym przypadku, skorzystać z podobieństwa trójkątów 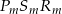 i
i 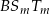 . Aby pole tego drugiego było równe 2, musi być
. Aby pole tego drugiego było równe 2, musi być
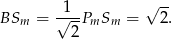
Z drugiej strony 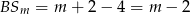 . Stąd
. Stąd
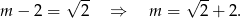
Odpowiedź: 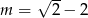 lub
lub