/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt/Dowolny/Dane są trzy wierzchołki

Zadanie nr 4322082

Napisz równanie okręgu opisanego na trójkącie o wierzchołkach 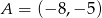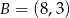A = (− 8,− 5) , B = (8,3) i C = (6,9) .

Wersja PDF

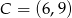Rozwiązanie

Zaczynamy od szkicowego rysunku.

PIC

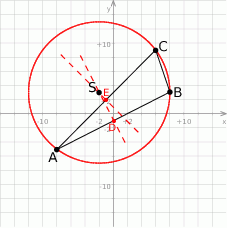
Sposób I

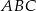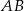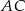Aby wyznaczyć środek okręgu opisanego napiszemy równania dwóch symetralnych boków trójkąta ABC i znajdziemy ich punkt wspólny. Środki boków AB i AC trójkąta 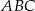ABC mają współrzędne

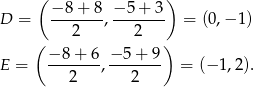
( −8 + 8 − 5+ 3) D = -------,------- = (0,− 1) ( 2 2 ) − 8 + 6 −5 + 9 E = -------, ------- = (− 1,2). 2 2

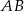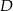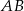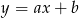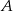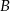Chcemy teraz napisać równanie prostej prostopadłej do AB i przechodzącej przez D . Najpierw piszemy równanie prostej AB – szukamy prostej w postaci y = ax+ b . Podstawiając współrzędne punktów A i B mamy układ równań

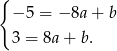
{ − 5 = − 8a + b 3 = 8a + b.

Odejmując od drugiego równania pierwsze (żeby zredukować 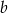b ) otrzymujemy

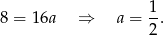
8 = 16a ⇒ a = 1-. 2

Współczynnika 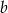b nie wyliczamy, bo nie jest nam potrzebny. Symetralna boku 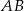AB jest prostopadła do prostej 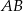AB , więc ma współczynnik kierunkowy -2 i prosta ta ma postać 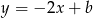y = − 2x + b . Współczynnik 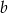b wyliczamy podstawiając współrzędne punktu D .

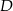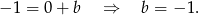
− 1 = 0+ b ⇒ b = − 1.

W takim razie prosta 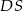DS ma równanie y = − 2x− 1 .

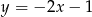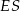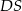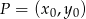
Równanie prostej ES moglibyśmy napisać dokładnie w ten sam sposób w jaki napisaliśmy równanie prostej DS , ale my dla urozmaicenia skorzystamy ze wzoru na równanie prostej prostopadłej do wektora → v = [p ,q] i przechodzącej przez punkt P = (x ,y ) 0 0

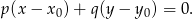
p(x − x ) + q(y − y ) = 0 . 0 0

W naszej sytuacji

→ −→ v = AC = [6+ 8,9+ 5] = [14,14].

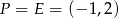i P = E = (− 1,2 ) . Zatem prosta 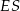ES ma więc równanie

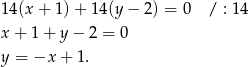
14(x + 1) + 14 (y− 2) = 0 / : 14 x + 1 + y − 2 = 0 y = −x + 1 .

Teraz wyznaczamy współrzędne punktu 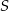S .

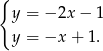
{ y = − 2x − 1 y = −x + 1.

Odejmując od drugiego równania pierwsze (żeby zredukować 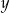y ) mamy

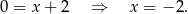
0 = x + 2 ⇒ x = − 2.

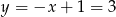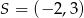Zatem y = −x + 1 = 3 i S = (− 2,3) . Żeby napisać równanie okręgu musimy jeszcze wyliczyć promień okręgu.

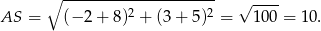
∘ --------------------- 2 2 √ ---- AS = (−2 + 8 ) + (3 + 5) = 100 = 10.

Okrąg opisany na trójkącie 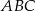ABC ma więc równanie

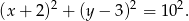
(x + 2)2 + (y − 3)2 = 102.

Sposób II

Szukamy równania okręgu opisanego w postaci

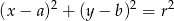
(x − a)2 + (y− b)2 = r2

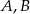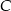Podstawiając do tego równania współrzędne punktów A ,B i C otrzymamy układ równań

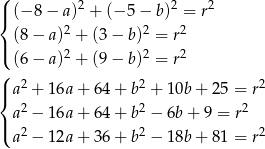
( | (− 8 − a)2 + (− 5 − b)2 = r2 { 2 2 2 | (8 − a ) + (3 − b) = r ( (6 − a )2 + (9 − b)2 = r2 ( |{ a 2 + 16a + 64+ b2 + 1 0b+ 25 = r2 2 2 2 |( a − 16a + 64+ b − 6b + 9 = r a 2 − 12a + 36+ b2 − 1 8b+ 81 = r2

Teraz odejmujemy od pierwszego równania drugie i odejmujemy od pierwszego równania trzecie – otrzymamy w ten sposób układ dwóch równań z dwoma niewiadomymi, w którym nie będzie już kwadratów.

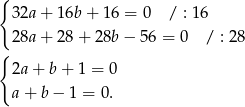
{ 32a + 16b + 16 = 0 / : 1 6 28a + 28 + 28b − 56 = 0 / : 28 { 2a + b+ 1 = 0 a+ b− 1 = 0.

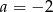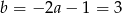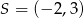Odejmując od pierwszego równania drugie mamy a = − 2 . Zatem b = −2a − 1 = 3 i S = (− 2,3 ) . Promień okręgu wyliczamy z pierwszego równania wyjściowego układu.

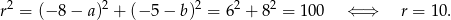
2 2 2 2 2 r = (− 8 − a) + (− 5− b) = 6 + 8 = 100 ⇐ ⇒ r = 10.

 
Odpowiedź: (x + 2)2 + (y − 3)2 = 10 2

Wersja PDF