/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt/Dowolny/Dane są trzy wierzchołki

Zadanie nr 4451780

Dodaj do ulubionych
Dodaj do rozwiązanych

Dane są punkty 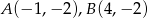A (−1 ,−2 ),B(4,− 2) oraz C(− 1 ,4 ) .

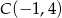  • Za pomocą odpowiedniego układu nierówności opisz trójkąt ABC .
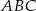  • Oblicz odległość punktu 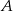A od prostej BC .
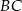  • Oblicz promień koła wpisanego w trójkąt ABC .
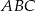  • Wyznacz równanie symetralnej boku BC .

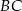Rozwiązanie

Jeżeli naszkicujemy sobie dany trójkąt, to widać, że jest to trójkąt prostokątny.

PIC

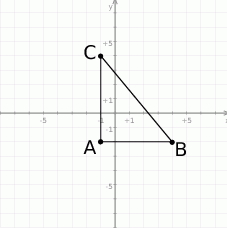
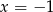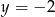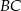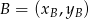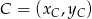  • Równania dwóch jego boków widać z rysunku: x = − 1 i y = − 2 . Wyznaczmy równanie boku BC . Korzystamy ze wzoru na równanie prostej przechodzącej przez dwa punkty B = (xB ,yB ) i C = (xC,yC ) :
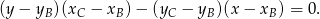
    (y− yB)(xC − xB )− (yC − yB)(x − xB ) = 0.

    W naszej sytuacji mamy

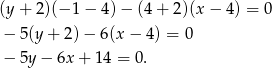
    (y+ 2)(− 1− 4)− (4+ 2)(x− 4) = 0 − 5(y+ 2)− 6(x − 4) = 0 − 5y− 6x + 14 = 0 .

    Zatem trójkąt 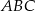ABC jest opisany układem nierówności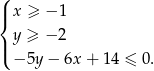

    ( |{ x ≥ − 1 y ≥ − 2 |( − 5y − 6x + 14 ≤ 0.
  •  

    Sposób I

    Z obrazka widać, że pole trójkąta jest równe

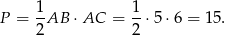
    1 1 P = -AB ⋅AC = --⋅5 ⋅6 = 15. 2 2

    Obliczmy długość przeciwprostokątnej.

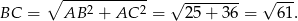
    ------------ ∘ 2 2 √ -------- √ --- BC = AB + AC = 2 5+ 36 = 61.

    Odległość punktu 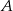A od prostej 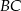BC to wysokość 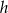h trójkąta 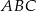ABC , więc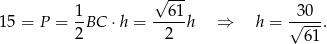

    1 √ 61- 30 15 = P = -BC ⋅ h = -----h ⇒ h = √---. 2 2 61

    Sposób II

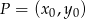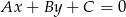    Korzystamy ze wzoru na odległość punktu P = (x0,y0) od prostej Ax + By + C = 0 :

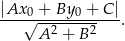
    |Ax√0 +-By0-+-C-| A 2 + B2 .

    W naszej sytuacji mamy

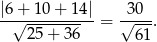
    |6+√--10+--14| √30-- 25+ 36 = 61 .

     
    Odpowiedź: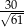 √3601-

  • Korzystamy z obliczeń z poprzedniego podpunktu:
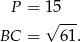
    P = 15 √ --- BC = 61 .

    Promień okręgu wpisanego możemy wyliczyć ze wzoru na pole 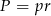P = pr , gdzie 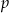p jest połową obwodu. Mamy zatem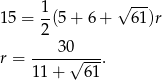

    1 √ --- 1 5 = --(5+ 6 + 6 1)r 2 r = ---3-0√---. 11 + 61

     
    Odpowiedź: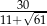 30 11+√-61-

  • Środek boku 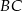BC ma współrzędne 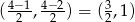( 4−21, 4−22) = (32,1) . Najprościej jest teraz skorzystać ze wzoru na równanie prostej prostopadłej do wektora → v = [p,q] i przechodzącej przez punkt (x0,y0)
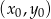
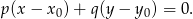
    p (x− x0)+ q(y− y0) = 0.

    U nas → → v = BC = [− 5,6] , zatem

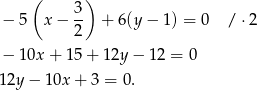
    ( ) − 5 x − 3- + 6(y − 1) = 0 / ⋅2 2 − 10x + 15 + 12y − 1 2 = 0 12y − 10x + 3 = 0.

     
    Odpowiedź: 12y − 10x + 3 = 0

Wersja PDF