/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt/Dowolny/Dane są trzy wierzchołki

Zadanie nr 5524248

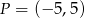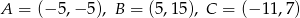Sprawdź czy punkt P = (− 5,5) jest środkiem okręgu wpisanego w trójkąt o wierzchołkach A = (−5 ,−5 ), B = (5,15), C = (− 11 ,7) .

Wersja PDF

Rozwiązanie

Jak ustalić, czy punkt 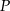P jest środkiem okręgu wpisanego? – wystarczy sprawdzić, czy 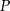P jest równoodległy od wszystkich boków trójkąta ABC .

PIC

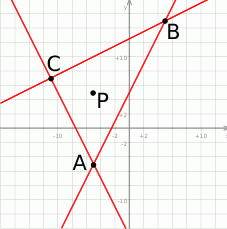
Napiszmy równania prostych zawierających jego boki. Można to zrobić korzystając ze wzoru na równanie prostej przechodzącej przez dwa punkty, ale można też bezpośrednio.

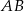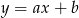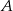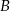Zacznijmy od prostej AB . Szukamy prostej postaci y = ax + b . Wstawiając współrzędne punktów A i B otrzymujemy układ równań.

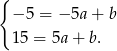
{ − 5 = − 5a + b 15 = 5a + b.

Odejmując od drugiego równania pierwsze (żeby skrócić 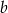b ) otrzymujemy

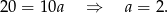
2 0 = 10a ⇒ a = 2.

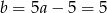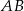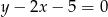Zatem b = 5a − 5 = 5 i prosta AB ma równanie y − 2x − 5 = 0 .

Szukamy teraz prostej 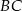BC . Jak poprzednio, otrzymujemy układ równań

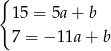
{ 15 = 5a+ b 7 = − 11a + b

Tym razem odejmujemy od pierwszego równania drugie i mamy

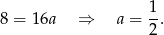
1 8 = 16a ⇒ a = --. 2

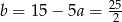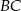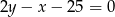Zatem 25 b = 15 − 5a = 2 i prosta BC ma równanie 2y − x− 25 = 0 .

Teraz szukamy prostej 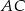AC . Mamy układ

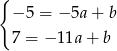
{ − 5 = − 5a + b 7 = − 11a + b

Odejmując od pierwszego równania drugie mamy

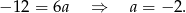
− 12 = 6a ⇒ a = − 2.

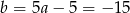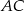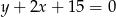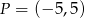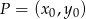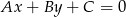Stąd b = 5a − 5 = −1 5 i prosta AC ma równanie y+ 2x+ 15 = 0 . Teraz pozostało sprawdzić jaka jest odległość punktu P = (−5 ,5) od każdej z tych prostych. Korzystamy ze wzoru na odległość punktu P = (x 0,y 0) od prostej Ax + By + C = 0 :

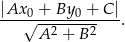
|Ax-0√-+-By-0 +-C|. A 2 + B 2

Zatem odległość punktu 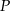P od kolejnych prostych jest równa

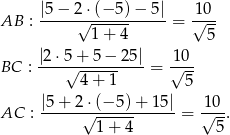
|5-−-2-⋅(−-5)-−-5|- -10- AB : √ 1+--4- = √ 5- BC : |2-⋅5√-+-5−-25| = √10-- 4 + 1 5 |5+ 2 ⋅(− 5) + 15| 10 AC : -----√-------------= √--. 1 + 4 5

Zatem istotnie punkt 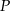P jest równoodległy od wszystkich boków trójkąta 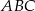ABC , więc jest środkiem okręgu wpisanego.  
Odpowiedź: Tak, jest to środek okręgu wpisanego

Wersja PDF