Zadanie nr 6413632
Uzasadnij, że koło o środku 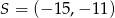 i promieniu
i promieniu 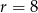 jest w całości zawarte w trójkącie o wierzchołkach
jest w całości zawarte w trójkącie o wierzchołkach 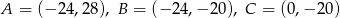 .
.
Rozwiązanie
Wprawdzie podane liczby są dość duże, ale możemy sobie naszkicować opisaną sytuację.
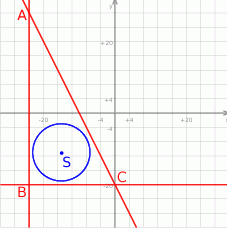
Z obrazka widać, że łatwo napisać równania dwóch boków trójkąta:
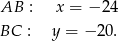
Zauważmy jeszcze, że punkt 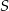 leży na prawo od prostej
leży na prawo od prostej 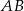 i powyżej prostej
i powyżej prostej  .
.
Napiszmy teraz równanie boku 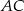 . Skorzystamy ze wzoru na równanie prostej przechodzącej przez dwa punkty
. Skorzystamy ze wzoru na równanie prostej przechodzącej przez dwa punkty 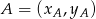 i
i 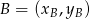 :
:
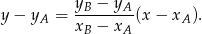
Stosujemy ten wzór dla 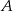 i
i 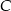 :
:
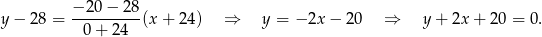
Zauważmy teraz (wstawiając współrzędne punktu 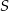 do równania prostej
do równania prostej 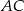 ), że punkt
), że punkt 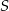 leży poniżej prostej
leży poniżej prostej 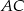 . To oznacza, że punkt
. To oznacza, że punkt 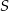 leży wewnątrz trójkąta
leży wewnątrz trójkąta 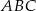 .
.
Powinno być jasne, że wystarczy pokazać, iż podane koło nie przecina prostych zawierających boki trójkąta 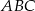 . Aby to wykazać, wystarczy sprawdzić, że środek tego koła jest odległy od boków trójkąta o więcej niż promień
. Aby to wykazać, wystarczy sprawdzić, że środek tego koła jest odległy od boków trójkąta o więcej niż promień 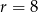 .
.
Odległość punktu 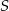 od prostych
od prostych 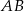 i
i 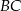 to odpowiednio
to odpowiednio
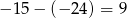
oraz
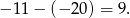
Obie te liczby są większe od 8, więc podany okrąg nie przecina tych prostych. Pozostało sprawdzić bok 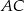 . Liczymy odległość punktu
. Liczymy odległość punktu 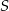 od tej prostej.
od tej prostej.
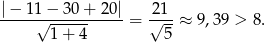
Zatem okrąg nie przecina też boku 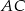 .
.

