/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt/Dowolny/Dane są trzy wierzchołki

Zadanie nr 6896340

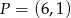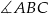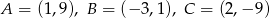Sprawdź czy punkt P = (6,1) leży na dwusiecznej kąta ∡ABC trójkąta o wierzchołkach A = (1,9), B = (− 3,1), C = (2,− 9) .

Wersja PDF

Rozwiązanie

Możemy zacząć od szkicowego rysunku.

PIC

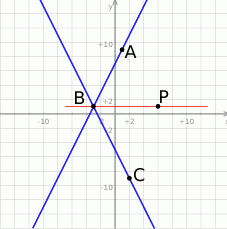
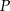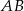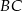Dwusieczna kąta to zbiór punktów, które są jednakowo odległe od obu ramion kąta, musimy więc sprawdzić czy punkt P jest równoodległy od prostych AB i BC . Zacznijmy od wyznaczenia równań tych prostych. Można to zrobić ze wzoru na równanie prostej przez dwa punkty, ale my to zrobimy wprost.

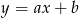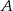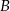Szukamy prostej w postaci y = ax+ b . Wstawiając do tego równania współrzędne punktów A i B mamy układ równań

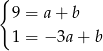
{ 9 = a + b 1 = − 3a + b

Odejmując od pierwszego równania drugie (żeby skrócić 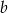b ) mamy

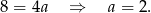
8 = 4a ⇒ a = 2.

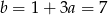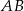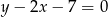Zatem b = 1 + 3a = 7 i prosta AB ma równanie y − 2x − 7 = 0 .

Podobnie wyznaczamy równanie prostej 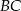BC . Mamy układ

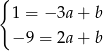
{ 1 = − 3a + b − 9 = 2a + b

Tym razem odejmujemy od drugiego równania pierwsze i mamy

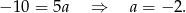
− 10 = 5a ⇒ a = − 2.

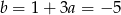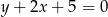Stąd b = 1 + 3a = −5 i prosta BC ma równanie y + 2x + 5 = 0 .

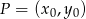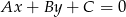Teraz pozostało policzyć odległość punktu P od tych prostych. Korzystamy ze wzoru na odległość punktu P = (x0,y0) od prostej Ax + By + C = 0 :

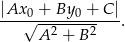
|Ax-0-+-By-0 +-C|- √ --2----2- . A + B

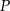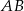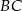Zatem odległość punktu P od prostych AB i BC jest odpowiednio równa

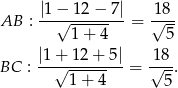
|1− 12 − 7| 18 AB :--√--------- = √--- 1 + 4 5 |1+ 12+ 5| 18 BC : --√---------= √---. 1 + 4 5

Ponieważ odległości te są równe, punkt 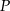P leży na dwusiecznej kata ∡B .  
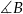Odpowiedź: Tak, punkt 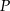P leży na tej dwusiecznej.

Wersja PDF