/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt/Dowolny/Dane są trzy wierzchołki

Zadanie nr 9396681

Dane są punkty 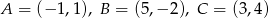A = (− 1,1), B = (5,− 2), C = (3 ,4) .

  • Wyznacz równanie prostej przechodzącej przez punkt 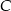C i prostopadłej do prostej AB .
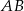  • Oblicz pole trójkąta ABC .
Wersja PDF

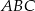Rozwiązanie

Zaczynamy od rysunku.

PIC

  •  

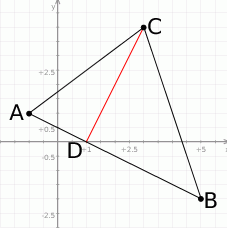
    Sposób I

    Najprościej jest skorzystać ze wzoru na równanie prostej prostopadłej do wektora → v = [p ,q] i przechodzącej przez punkt (x 0,y0)

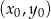
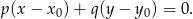
    p (x− x )+ q(y− y ) = 0. 0 0

    W naszej sytuacji mamy → → v = AB = [6,− 3] , skąd szukane równanie to

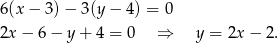
    6(x− 3)− 3(y− 4) = 0 2x− 6− y+ 4 = 0 ⇒ y = 2x − 2.

    Sposób II

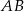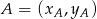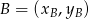    Jak ktoś nie lubi wektorów, to może to zrobić bardziej tradycyjnie. Najpierw piszemy równanie prostej AB . Korzystamy ze wzoru na równanie prostej przechodzącej przez dwa punkty A = (xA,yA ) i B = (xB,yB) :

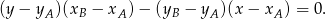
    (y − yA )(xB − xA )− (yB − yA)(x − xA ) = 0.

    W naszej sytuacji mamy

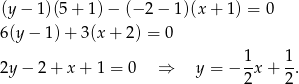
    (y − 1)(5 + 1) − (− 2 − 1)(x + 1) = 0 6(y − 1) + 3(x + 2) = 0 1- 1- 2y − 2 + x + 1 = 0 ⇒ y = − 2 x+ 2.

    Prosta prostopadła do tej prostej ma postać 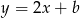y = 2x + b . Współczynnik 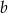b wyliczamy z tego, że przechodzi ona przez punkt C .

    4 = 2⋅ 3+ b ⇒ b = − 2.

     
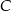    Odpowiedź: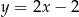 y = 2x − 2

  •  

    Sposób I

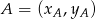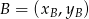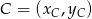    Korzystamy ze wzoru na pole trójkąta o wierzchołkach A = (xA ,yA) , B = (xB,yB) i C = (xC ,yC) .

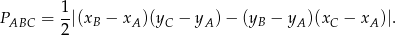
    1- PABC = 2|(xB − xA )(yC − yA )− (yB − yA)(xC − xA)|.

    W naszej sytuacji mamy

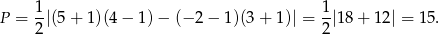
    P = 1-|(5 + 1 )(4 − 1 )− (− 2 − 1)(3 + 1)| = 1-|18+ 12| = 15. 2 2

    Sposób II

    Możemy też skorzystać z wyliczonej wcześniej prostej 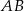AB . Znajdźmy jej punkt wspólny 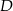D z wysokością poprowadzoną z wierzchołka 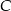C (którą wyliczyliśmy w poprzednim podpunkcie).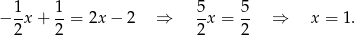

    1 1 5 5 − --x+ --= 2x− 2 ⇒ --x = -- ⇒ x = 1. 2 2 2 2

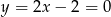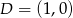    Stąd y = 2x − 2 = 0 i D = (1 ,0) . Liczymy teraz długości wysokości 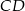CD i boku AB .

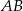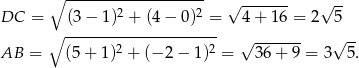
    ∘ ------------------- √ ------- √ -- DC = (3 − 1)2 + (4− 0)2 = 4 + 16 = 2 5 ∘ --------------------- √ ------- √ -- AB = (5+ 1)2 + (− 2− 1 )2 = 36 + 9 = 3 5 .

    Zatem pole jest równe

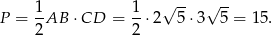
    1- 1- √ -- √ -- P = 2AB ⋅CD = 2 ⋅2 5 ⋅3 5 = 1 5.

    Sposób III

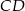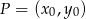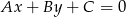    Mała modyfikacja poprzedniego sposobu. Długość wysokości CD mogliśmy wyliczyć ze wzoru na odległość punktu P = (x0,y0) od prostej Ax + By + C = 0 :

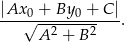
    |Ax + By + C | ---√0-----0------. A 2 + B2

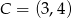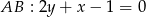    My stosujemy ten wzór dla punktu C = (3,4) i prostej AB : 2y+ x − 1 = 0 .

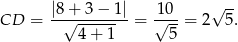
    CD = |8√+-3−--1| = √10-= 2√ 5. 4 + 1 5

    Dalej liczymy jak poprzednio.  
    Odpowiedź: 15

Wersja PDF