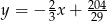Zadanie nr 9642655
Dane są wierzchołki trójkąta 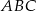 :
: 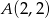 ,
, 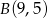 i
i 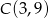 . Z wierzchołka
. Z wierzchołka 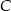 poprowadzono wysokość tego trójkąta, która przecina bok
poprowadzono wysokość tego trójkąta, która przecina bok 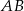 w punkcie
w punkcie 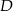 . Wyznacz równanie prostej przechodzącej przez punkt
. Wyznacz równanie prostej przechodzącej przez punkt 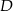 i równoległej do boku
i równoległej do boku 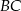 .
.
Rozwiązanie
Szkicujemy opisaną sytuację.
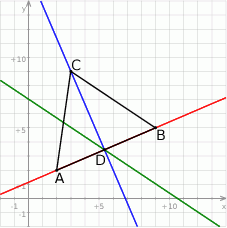
Aby wyznaczyć współrzędne punktu 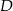 wyznaczamy najpierw równania prostych
wyznaczamy najpierw równania prostych 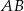 i
i 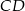 . Szukamy prostej
. Szukamy prostej 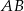 w postaci
w postaci 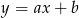 . Podstawiamy współrzędne punktów
. Podstawiamy współrzędne punktów 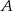 i
i 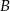 .
.
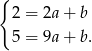
Odejmujemy od drugiego równania pierwsze (żeby skrócić 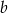 ) i mamy
) i mamy 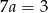 , czyli
, czyli 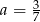 . Z pierwszego równania mamy więc
. Z pierwszego równania mamy więc
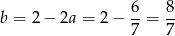
i prosta 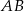 ma równanie
ma równanie 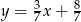 .
.
Prosta 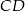 jest prostopadła do
jest prostopadła do 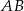 , więc ma równanie postaci
, więc ma równanie postaci 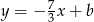 . Aby obliczyć
. Aby obliczyć 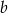 podstawiamy w tym równaniu współrzędne punktu
podstawiamy w tym równaniu współrzędne punktu 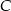 .
.
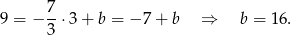
Szukamy teraz punktu wspólnego 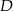 prostych
prostych 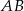 i
i 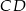 .
.
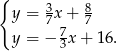
Odejmujemy od pierwszego równania drugie (żeby skrócić 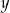 ) i mamy
) i mamy
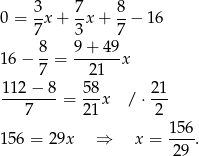
Z drugiego równania układu mamy
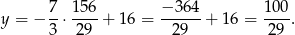
Zatem 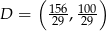 .
.
Szukamy teraz równania prostej 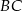 w postaci
w postaci 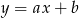 . Podstawiamy współrzędne punktów
. Podstawiamy współrzędne punktów 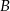 i
i 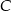 .
.
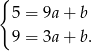
Odejmujemy od pierwszego równania drugie i mamy 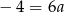 . Stąd
. Stąd 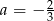 . Współczynnika
. Współczynnika 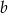 nie obliczamy, bo nie jest nam potrzebny.
nie obliczamy, bo nie jest nam potrzebny.
Szukana prosta równoległa do 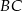 i przechodząca przez
i przechodząca przez 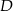 ma taki sam współczynnik kierunkowy jak prosta
ma taki sam współczynnik kierunkowy jak prosta 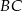 , więc jest postaci
, więc jest postaci 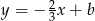 . Współczynnik
. Współczynnik 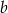 obliczamy podstawiając współrzędne punktu
obliczamy podstawiając współrzędne punktu 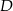 .
.
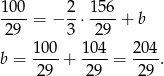
Szukana prosta ma więc równanie 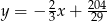 .
.
Odpowiedź: