/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt/Dowolny/Dane są trzy wierzchołki

Zadanie nr 9781513

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest trójkąt 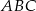ABC o wierzchołkach A = (1;4) , B = (5;2) , C = (3 ;− 3 ) .

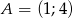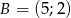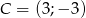  • Napisz równanie wysokości opuszczonej z wierzchołka 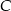C na bok AB .
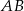  • Napisz równanie środkowej boku BC .
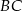  • Napisz równanie symetralnej boku BC .
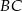  • Oblicz obwód i pole tego trójkąta.

Rozwiązanie

PIC

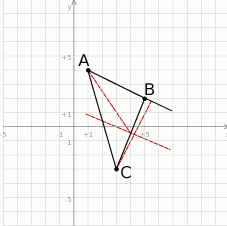
  • Najłatwiej jest skorzystać ze wzoru na równanie prostej prostopadłej do wektora → v = [p,q] i przechodzącej przez punkt (x0,y0)
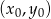
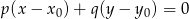
    p(x − x0) + q(y − y0) = 0

    W naszej sytuacji

    → → v = AB = [4 ,−2 ].

    Stąd szukane równanie to

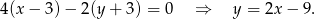
    4(x − 3) − 2(y + 3) = 0 ⇒ y = 2x − 9 .

     
    Odpowiedź: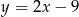 y = 2x − 9

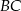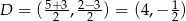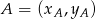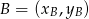  • Środek boku BC ma współrzędne D = (5+-3, 2−3) = (4,− 1) 2 2 2 . Korzystamy ze wzoru na równanie prostej przechodzącej przez dwa punkty A = (xA,yA ) i B = (xB,yB ) :
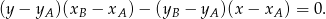
    (y − yA )(xB − xA )− (yB − yA)(x − xA ) = 0.

    Mamy zatem

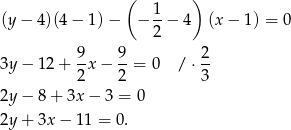
    ( 1 ) (y− 4)(4− 1)− − -− 4 (x − 1) = 0 2 9- 9- 2- 3y− 12 + 2 x− 2 = 0 / ⋅3 2y− 8+ 3x − 3 = 0 2y+ 3x − 11 = 0 .

     
    Odpowiedź: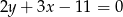 2y + 3x− 11 = 0

  • Ponownie korzystamy ze wzoru na równanie prostej przechodzącej przez punkt 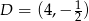D = (4,− 12) i prostopadłej do wektora → CB = [2 ,5 ]
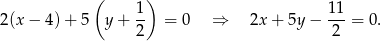
    ( ) 1- 11- 2 (x− 4)+ 5 y+ 2 = 0 ⇒ 2x + 5y − 2 = 0.

     
    Odpowiedź: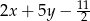 2x + 5y − 112

  • Liczymy długości boków.
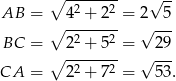
    ∘ --2----2 √ -- AB = ∘ 4--+-2- = 2 5 BC = 2 2 + 5 2 = √ 29 ∘ ------- √ --- CA = 2 2 + 7 2 = 53.

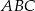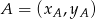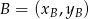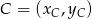    Aby obliczyć pole trójkąta ABC , korzystamy ze wzoru na pole trójkąta o wierzchołkach A = (xA ,yA ) , B = (xB,yB ) i C = (xC,yC ) .

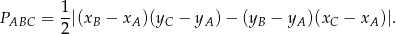
    1 PABC = -|(xB − xA )(yC − yA )− (yB − yA)(xC − xA)|. 2

    W naszej sytuacji

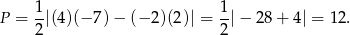
    1- 1- P = 2 |(4)(− 7)− (− 2)(2 )| = 2|− 28+ 4| = 12.

     
    Odpowiedź: Boki: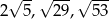 √ --√ ---√ --- 2 5, 29 , 53 , pole: 12.

Wersja PDF