Zadanie nr 9957996
Przekształcenie 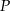 określone jest w następujący sposób:
określone jest w następujący sposób: 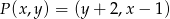 , gdzie
, gdzie 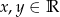 .
.
- Wykaż, że przekształcenie
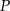 jest izometrią.
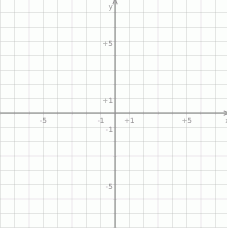
jest izometrią. - W prostokątnym układzie współrzędnych narysuj trójkąt o wierzchołkach
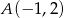 ,
, 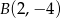 ,
, 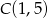 , a następnie znajdź jego obraz w przekształceniu
, a następnie znajdź jego obraz w przekształceniu 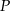 .
. - Wyznacz równanie prostej zawierającej wysokość trójkąta
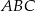 poprowadzoną na bok
poprowadzoną na bok 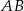 .
. - Oblicz pole trójkąta
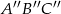 , który jest obrazem trójkąta
, który jest obrazem trójkąta 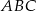 w jednokładności o środku w punkcie (0,0) i skali
w jednokładności o środku w punkcie (0,0) i skali 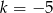 .
.
Rozwiązanie
-
Sposób I
Przekształcenie
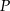 możemy rozpisać następująco
możemy rozpisać następująco 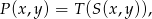
gdzie
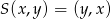 i
i 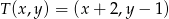 . Przekształcenie to jest zatem złożeniem symetrii względem prostej
. Przekształcenie to jest zatem złożeniem symetrii względem prostej 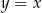 z przesunięciem (translacją) o wektor
z przesunięciem (translacją) o wektor ![[2,− 1]](https://img.zadania.info/zad/9957996/HzadR5x.gif) (najpierw symetria, potem translacja). Jest to więc izometria.
(najpierw symetria, potem translacja). Jest to więc izometria. Sposób II
Musimy sprawdzić, że przekształcenie to zachowuje odległość. Jeżeli
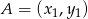 i
i 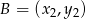 , to
, to 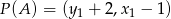 ,
, 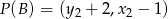 . Mamy zatem
. Mamy zatem 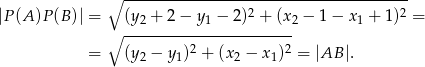
- Korzystając ze wzoru na
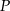 (z treści zadania), wyliczamy
(z treści zadania), wyliczamy 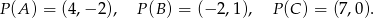
- Skorzystamy ze wzoru na równanie prostej prostopadłej do wektora
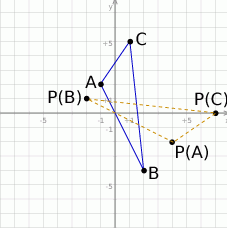
![→v = [p,q]](https://img.zadania.info/zad/9957996/HzadR14x.gif) i przechodzącej przez punkt
i przechodzącej przez punkt 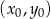
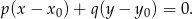
W naszej sytuacji
![→ →v = AB = [3 ,−6 ],](https://img.zadania.info/zad/9957996/HzadR17x.gif)
oraz
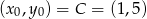 . Stąd szukana prosta to
. Stąd szukana prosta to 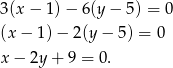
Odpowiedź: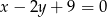
- Aby obliczyć pole trójkąta
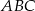 , korzystamy ze wzoru
, korzystamy ze wzoru 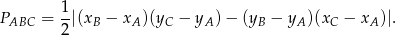
W naszej sytuacji
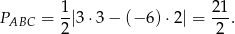
Ponieważ pole przy jednokładności zmienia się jak kwadrat skali (bo odcinki zmieniają się jak skala, a pole to iloczyn dwóch odcinków), to
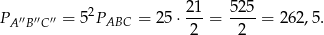
Odpowiedź: 262,5

