Zadanie nr 3103695
Dwie pracownice urzędu pocztowego miały ostemplować pewną partię listów. Stemplowanie listów pierwsza urzędniczka rozpoczęła o godzinie 8:00, a druga o godzinie 9:00. O godzinie 11:00 panie stwierdziły, że pozostało im jeszcze do ostemplowania 45% listów. Po ukończeniu pracy okazało się, że każda z urzędniczek ostemplowała tyle samo listów. Oblicz, w ciągu ilu godzin każda z pań ostemplowałaby sama wszystkie listy.
Rozwiązanie
Sposób I
Oznaczmy szukane czasy pracy urzędniczek przez 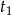 i
i 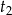 odpowiednio. Zatem w ciągu godziny panie stemplują odpowiednio
odpowiednio. Zatem w ciągu godziny panie stemplują odpowiednio 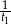 i
i 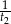 ogółu wszystkich listów.
ogółu wszystkich listów.
Jeżeli oznaczymy przez 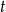 całkowity czas pracy pierwszej z pań, to ponieważ panie ostemplowały tyle samo listów mamy
całkowity czas pracy pierwszej z pań, to ponieważ panie ostemplowały tyle samo listów mamy
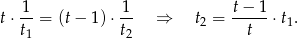
Ponadto razem ostemplowały
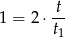
wszystkich listów (dwa razy więcej niż pierwsza z nich). Zatem 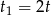 .
.
O godzinie 11:00 panie miały ostemplowane
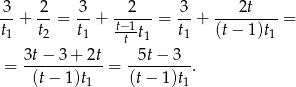
listów. Mamy zatem równanie
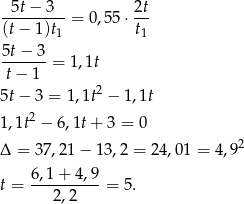
(Pomijamy ujemny pierwiastek.) Mamy więc 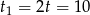 i
i
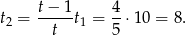
Sposób II
Oznaczmy przez  i
i 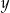 czas (w godzinach) potrzebny odpowiednio pierwszej i drugiej urzędniczce na ostemplowanie wszystkich listów. W ciągu jednej godziny stemplują one więc odpowiednio
czas (w godzinach) potrzebny odpowiednio pierwszej i drugiej urzędniczce na ostemplowanie wszystkich listów. W ciągu jednej godziny stemplują one więc odpowiednio  i
i 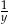 wszystkich listów. Wiemy, że do godziny 11 wykonały 55% całej pracy, czyli
wszystkich listów. Wiemy, że do godziny 11 wykonały 55% całej pracy, czyli
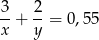
(pierwsza pracowała przez 3 godziny, a druga przez 2).
Wiemy ponadto, że na koniec dnia ostemplowały tyle samo listów, czyli każda z nich ostemplowała połowę całości. Taka praca zajmuje pierwszej urzędniczce  godzin, a drugiej
godzin, a drugiej 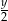 godzin, więc
godzin, więc
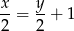
(bo pierwsza pracowała o godzinę dłużej). Z tego równania mamy
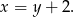
Podstawiamy to wyrażenie do pierwszego równania i mamy
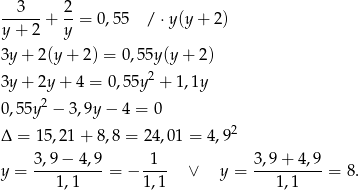
Ujemne rozwiązanie odrzucamy i mamy 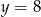 . Stąd
. Stąd 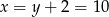 .
.
Odpowiedź: 10 i 8 godzin

