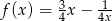Zadanie nr 8579529

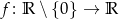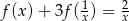Znajdź wszystkie funkcje f : R ∖{ 0} → R , dla których zachodzi równość f (x)+ 3f(1x) = 2x .

Rozwiązanie

Jeżeli podstawimy w danym równaniu 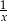1 x zamiast , to otrzymamy równość

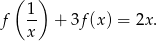
( ) f 1- + 3f(x ) = 2x. x

Wystarczy teraz potraktować 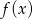f(x ) jako niewiadomą i rozwiązać układ równań

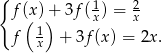
{ f(x) + 3f( 1) = 2 ( 1) x x f x + 3f (x) = 2x .

Jeżeli odejmiemy od pierwszego równania drugie pomnożone przez 3 (żeby skrócić 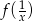f( 1) x ), to otrzymamy

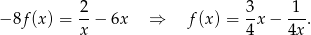
2 3 1 − 8f(x) = x-− 6x ⇒ f (x) = 4-x− 4x-.

Odpowiedź: 3 -1 f(x ) = 4x − 4x

Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!

Dodaj komentarz