/Szkoła średnia/Prawdopodobieństwo/Z definicji/Geometryczne

Zadanie nr 1380842

Dodaj do ulubionych
Dodaj do rozwiązanych

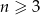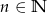Wielokąt wypukły ma n wierzchołków, n ≥ 3 , n ∈ N , spośród których losujemy jednocześnie dwa. Wyznacz n , wiedząc, że prawdopodobieństwo wylosowania wierzchołków wyznaczających przekątną tego wielokąta jest mniejsze od 4 5 .

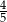Rozwiązanie

Przyjmijmy, że zdarzenia elementarne to dwuelementowe zbiory składające się z wierzchołków (pary nieuporządkowane). Zatem

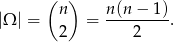
( ) |Ω | = n = n(n-−-1). 2 2

Para wierzchołków wielokąta wyznacza przekątną, jeżeli nie są one sąsiednie. Ile jest takich par? – od wszystkich trzeba odjąć n boków wielokąta. Zatem

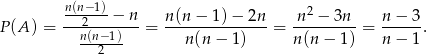
n(n−-1) 2 P(A ) = ---2---−-n- = n-(n-−-1)−--2n = n--−-3n--= n-−-3-. n(n−-1) n(n − 1) n(n − 1) n − 1 2

Pozostało sprawdzić kiedy 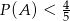P(A ) < 4 5 .

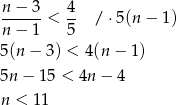
n-−-3- 4- n − 1 < 5 / ⋅5(n − 1) 5(n − 3) < 4 (n− 1) 5n − 15 < 4n − 4 n < 1 1

Tak więc 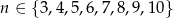n ∈ { 3,4,5,6,7,8,9,1 0} .

Wersja PDF