Zadanie nr 2434343

Losujemy dwa różne punkty spośród wierzchołków sześcianu o boku długości 1. Jakie jest prawdopodobieństwo, że

Rozwiązanie

Przyjmijmy za zdarzenia sprzyjające dwuelementowe zbiory wylosowanych wierzchołków (czyli odcinki łączące dwa wierzchołki sześcianu).

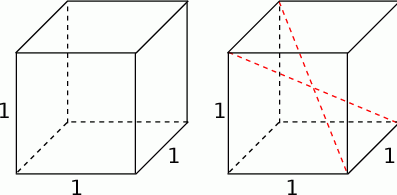
Mamy zatem

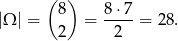
( ) |Ω | = 8 = 8-⋅7 = 2 8. 2 2

Zdarzeń sprzyjających jest tyle, ile jest krawędzi sześcianu (bo tylko krawędzie mają długość 1), czyli 12. Zatem szukane prawdopodobieństwo wynosi
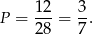
$12 3 P = ---= -. 28 7$

Odpowiedź:
Ponieważ przekątna ściany sześcianu ma długość 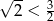, więc interesują nas tylko przekątne sześcianu, które mają długość 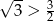. Takie przekątne są 4 (na obrazku narysowane są 2). Zatem szukane prawdopodobieństwo wynosi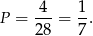
$P = -4-= 1. 28 7$

Odpowiedź:

Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!

Dodaj komentarz