Zadanie nr 6040940
Jakie jest prawdopodobieństwo tego, że losowo wybrane 4 różne wierzchołki sześcianu są wierzchołkami czworościanu foremnego?
Rozwiązanie
Przyjmijmy, że zdarzenia elementrane to nieuporządkowane wybory czterech wierzchołków. Zatem
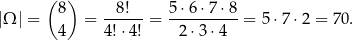
Jeżeli narysujemy sobie sześcian, to łatwo widać, że są tylko dwa takie czworościany (każdy taki czworościan, jest całkowicie wyznaczony przez jeden ze swoich wierzchołków, a wierzchołki są cztery, zatem są co najwyżej dwa takie czworościany).
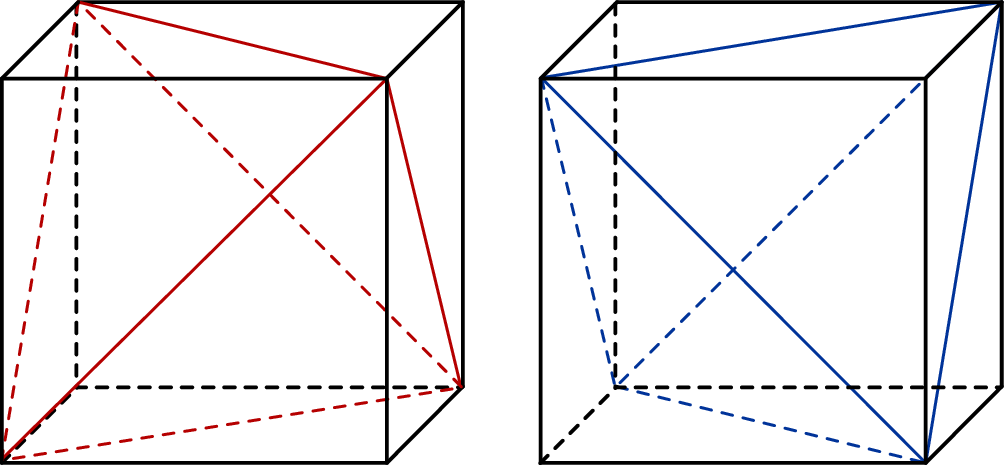
Zatem
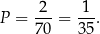
Odpowiedź: