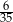Zadanie nr 6148316
Rozważmy zbiór wszystkich czteroelementowych podzbiorów zbioru wierzchołków pewnego prostopadłościanu. Oblicz prawdopodobieństwo wylosowania takiego podzbioru, którego elementy są wierzchołkami prostokąta.
Rozwiązanie
Jeżeli za zdarzenia elementarne przyjmiemy zbiory wylosowanych wierzchołków to
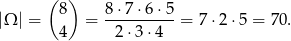
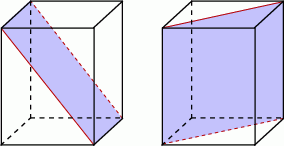
Zdarzenia sprzyjające liczymy ręcznie. Jest 6 ścian, oraz 6 prostokątów przechodzących przez środek prostopadłościanu i łączących równoległe krawędzie z przeciwległych ścian (każdy taki prostokąt jest wyznaczony przez przekątną ściany, więc jest ich=połowa wszystkich przekątnych ścian=6).
Zatem prawdopodobieństwo wynosi
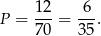
Odpowiedź: